题目内容
19.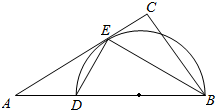 如图,在Rt△ABC中,∠C=90°,B E平分∠A BC交 AC于点E,点D在AB上,DE⊥EB,且${A}D=2\sqrt{3}$,AE=6.
如图,在Rt△ABC中,∠C=90°,B E平分∠A BC交 AC于点E,点D在AB上,DE⊥EB,且${A}D=2\sqrt{3}$,AE=6.(I)判断直线 AC与△BDE的外接圆的位置关系并说明理由;
(II)求EC的长.
分析 (I)取BD的中点0,连结OE,如图,由∠BED=90°,根据圆周角定理可得BD为△BDE的外接圆的直径,点O为△BDE的外接圆的圆心,再证明OE∥BC,得到∠AEO=∠C=90°,于是可根据切线的判定定理判断AC是△BDE的外接圆的切线;
(II)设⊙O的半径为r,根据勾股定理得${({r+2\sqrt{3}})^2}={r^2}+{6^2}$,解得r=2$\sqrt{3}$,根据平行线分线段成比例定理,由OE∥BC得$\frac{AE}{CE}$=$\frac{AO}{OB}$,然后根据比例性质可计算出EC.
解答 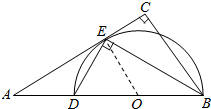 解:(I)取BD的中点0,连结OE,如图,
解:(I)取BD的中点0,连结OE,如图,
∵DE⊥EB,
∴∠BED=90°,
∴BD为△BDE的外接圆的直径,点O为△BDE的外接圆的圆心,
∵BE平分∠ABC,
∴∠CBE=∠OBE,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠OEB=∠CBE,
∴OE∥BC,
∴∠AEO=∠C=90°,
∴OE⊥AE,
∴AC是△BDE的外接圆的切线.
(II)设△BDE的外接圆的半径为r.
在△AOE中,OA2=OE2+AE2,即${({r+2\sqrt{3}})^2}={r^2}+{6^2}$,解得$r=2\sqrt{3}$,
∵OE∥BC,
∴$\frac{AE}{CE}$=$\frac{AO}{OB}$,即$\frac{6}{CE}$=$\frac{4\sqrt{3}}{2\sqrt{3}}$,
∴CE=3.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了勾股定理和平行线分线段成比例定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知$\overrightarrow a=(-3,2,5),\overrightarrow b=(1,5,-1),则\overrightarrow a•\overrightarrow b$=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
10.已知点M(3,-2),N(-5,-1),且$\overrightarrow{MP}=\frac{1}{2}\overrightarrow{MN}$,则点P是( )
| A. | (-8,1) | B. | (-1,-$\frac{3}{2}$) | C. | (1,$\frac{3}{2}$) | D. | (8,1) |
7.已知复数${z_1}=\frac{1}{2}-\frac{{\sqrt{3}i}}{2}$和复数z2=cos30°+isin30°,则z1•z2为( )
| A. | 1 | B. | -1 | C. | $-\frac{1}{2}i$ | D. | $\frac{{\sqrt{3}}}{2}-\frac{1}{2}i$ |
4.函数f(x)满足对定义域内的任意x,都有f(x+2)+f(x)<2f(x+1),则函数f(x)可以是( )
| A. | f(x)=lnx | B. | f(x)=x2-2x | C. | f(x)=ex | D. | f(x)=2x+1 |
11.已知函数f(x)=$\left\{\begin{array}{l}{x+1,(-1≤x≤0)}\\{cosx,(0<x≤\frac{π}{2})}\end{array}\right.$,则${∫}_{-1}^{\frac{π}{2}}$f(x)dx=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | $\frac{3}{2}$ |