题目内容
.(13分)已知等差数列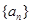 中,公差
中,公差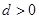 ,其前
,其前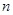 项和为
项和为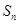 ,且满足
,且满足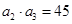 ,
,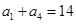 .
.
(1)求数列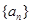 的通项公式;
的通项公式;
(2)设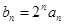 (
(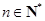 ),求数列
),求数列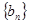 的前
的前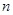 项和
项和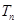 ;
;
(3)设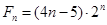 ,试比较
,试比较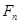 与
与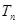 的大小.
的大小.
 中,公差
中,公差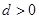 ,其前
,其前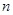 项和为
项和为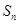 ,且满足
,且满足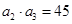 ,
,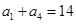 .
.(1)求数列
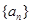 的通项公式;
的通项公式;(2)设
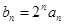 (
(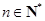 ),求数列
),求数列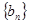 的前
的前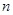 项和
项和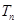 ;
;(3)设
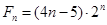 ,试比较
,试比较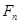 与
与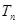 的大小.
的大小.解:(1)由已知可得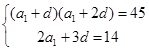 (
(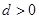 ) 解得
) 解得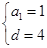
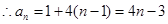 …………………………………………(4分)
…………………………………………(4分)
或:由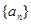 为等差数列得:
为等差数列得: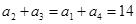 ,又
,又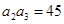 ,
,
故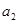 、
、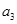 可以看作方程
可以看作方程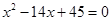 的两根,由
的两根,由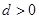 得
得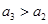
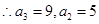 故
故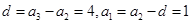
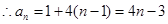 …………………………(4分)
…………………………(4分)
(2)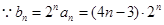
(3)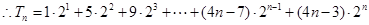 ?
?
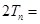
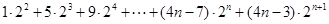 ?
?
?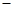 ?得:
?得:
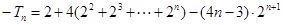
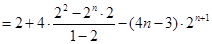
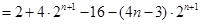

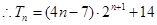 …………………(9分)
…………………(9分)
(3)
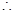 当
当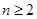 时,
时,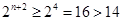 ,即
,即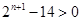 故
故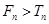
当 时,
时,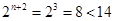 ,即
,即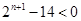 故
故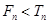
 综上可得,当
综上可得,当 时,
时,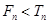 ;当
;当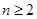 时,
时,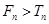 .………(13分)
.………(13分)
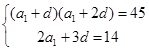 (
(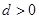 ) 解得
) 解得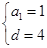
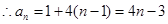 …………………………………………(4分)
…………………………………………(4分)或:由
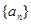 为等差数列得:
为等差数列得: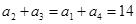 ,又
,又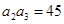 ,
,故
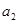 、
、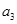 可以看作方程
可以看作方程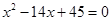 的两根,由
的两根,由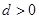 得
得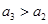
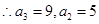 故
故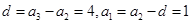
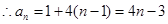 …………………………(4分)
…………………………(4分)(2)
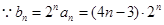
(3)
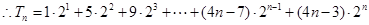 ?
?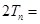
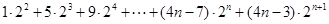 ?
??
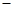 ?得:
?得: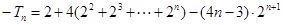
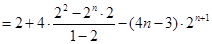
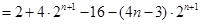

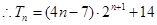 …………………(9分)
…………………(9分)(3)

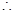 当
当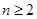 时,
时,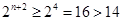 ,即
,即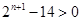 故
故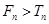
当
 时,
时,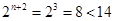 ,即
,即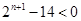 故
故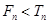
 综上可得,当
综上可得,当 时,
时,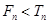 ;当
;当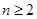 时,
时,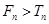 .………(13分)
.………(13分)略

练习册系列答案
相关题目
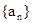 的公差
的公差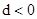 , 若
, 若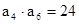 ,
, 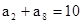 , 则该数列的前n项和
, 则该数列的前n项和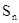 的最大值为 ( )
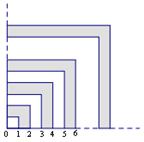
的最大值为 ( ) 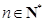 )的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、……、第n个阴影部分图形.设前n个阴影部分图形的面积的平均值为
)的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、……、第n个阴影部分图形.设前n个阴影部分图形的面积的平均值为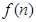 .记数列
.记数列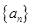 满足
满足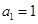 ,
,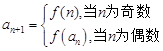
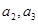 的值,并求数列
的值,并求数列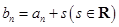 ,若不等式
,若不等式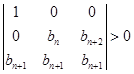 有解,求
有解,求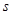 的取值范围.
的取值范围.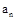 }的前n项和为
}的前n项和为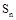 ,数列
,数列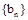 的前n项和为
的前n项和为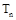 ,
,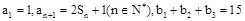
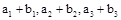 成等比数列,求
成等比数列,求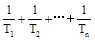
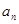 }中,
}中,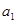 =" 8" ,
=" 8" ,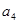 =" 2" ,且满足
=" 2" ,且满足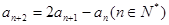 .
.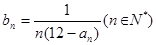 ,
,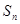 =
= 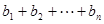 ,是否存在最大的整数m ,使得对任意的
,是否存在最大的整数m ,使得对任意的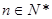 ,都有
,都有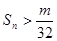 成立?若存在,求出m的值;若不存在,请说明理由 .
成立?若存在,求出m的值;若不存在,请说明理由 .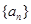 中,若
中,若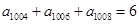 ,则该数列的前2011项的和为
,则该数列的前2011项的和为 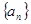 为等差数列,若
为等差数列,若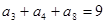 ,则
,则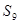 =( )
=( )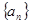 是等差数列,且
是等差数列,且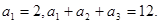
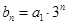 ,求
,求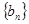 的前n项和.
的前n项和.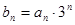 ,求
,求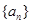 中,有
中,有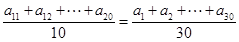 ,则在等比数列
,则在等比数列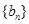 中,会有类似的结论_____________。
中,会有类似的结论_____________。