题目内容
已知数列{an}的通项公式an=n2cosnπ，Sn为它的前n项的和，则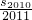
=
- A.1005
- B.1006
- C.2009
- D.2010
A
分析：根据an=n2cosnπ，可得an=（-1）n×n2，进而S2010=-12+22-32+42-…-20092+20102，两两合并，即可得到结论．
解答：∵an=n2cosnπ，∴an=（-1）n×n2，
∴S2010=-12+22-32+42-…-20092+20102=（2+1）（2-1）+（4+3）（4-3）+…+（2010+2009）（2010-2009）
=3+7+11+…+4019=
=1005×2011
∴
=1005
故选A．
点评：本题考查数列的求和，考查学生分析解决问题的能力，属于中档题．
分析：根据an=n2cosnπ，可得an=（-1）n×n2，进而S2010=-12+22-32+42-…-20092+20102，两两合并，即可得到结论．
解答：∵an=n2cosnπ，∴an=（-1）n×n2，
∴S2010=-12+22-32+42-…-20092+20102=（2+1）（2-1）+（4+3）（4-3）+…+（2010+2009）（2010-2009）
=3+7+11+…+4019=
=1005×2011∴
=1005故选A．
点评：本题考查数列的求和，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
已知数列{an}的通项为an=2n-1，Sn为数列{an}的前n项和，令bn=
，则数列{bn}的前n项和的取值范围为（ ）
| 1 |
| Sn+n |
A、[
| ||||
B、(
| ||||
C、[
| ||||
D、[
|