题目内容
已知抛物线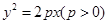 上的任意一点
上的任意一点 到该抛物线焦点的距离比该点到
到该抛物线焦点的距离比该点到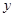 轴的距离多1.
轴的距离多1.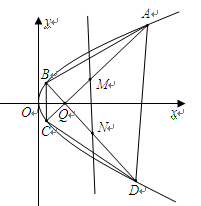
(1)求 的值;
的值;
(2)如图所示,过定点 (2,0)且互相垂直的两条直线
(2,0)且互相垂直的两条直线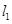 、
、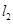 分别与该抛物线分别交于
分别与该抛物线分别交于 、
、 、
、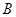 、
、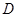 四点.
四点.
(i)求四边形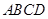 面积的最小值;
面积的最小值;
(ii)设线段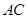 、
、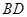 的中点分别为
的中点分别为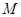 、
、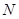 两点,试问:直线
两点,试问:直线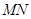 是否过定点?若是,求出定点坐标;若不是,请说明理由.
是否过定点?若是,求出定点坐标;若不是,请说明理由.
(1)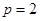 (2)(i)四边形
(2)(i)四边形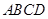 面积的最小值是48(ii)
面积的最小值是48(ii)
解析试题分析:(1)直接利用抛物线的定义
(2)(i)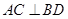 S四边形ABCD,
S四边形ABCD,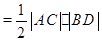 ,利用弦长
,利用弦长
公式,以及基本不等式,二次函数在闭区间上的最值问题
的解法求解
(ii)恒过定点问题的常规解法
试题解析:
(1)由已知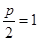 ∴
∴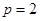
(2)(i)由题意可设直线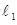 的方程为
的方程为 (
(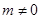 ),代入
),代入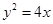 得
得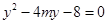
设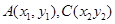 则
则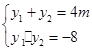 ,
,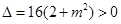
∴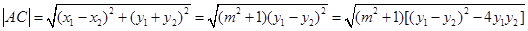
 6分
6分
同理可得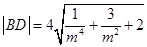 7分
7分
S四边形ABCD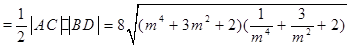
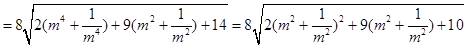 8分
8分
设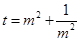 则
则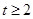 ∴S四边形ABCD
∴S四边形ABCD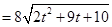
∵函数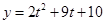 在
在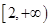 上是增函数
上是增函数
∴S四边形ABCD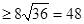 ,当且仅当即
,当且仅当即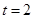 即
即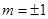 时取等号
时取等号
∴四边形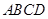 面积的最小值是48. 9分
面积的最小值是48. 9分
(ii)由①得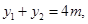 ∴
∴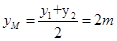 ∴
∴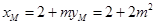
∴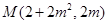 , 11分
, 11分
同理得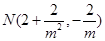 12分
12分
∴直线的方程可表示为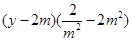
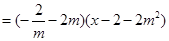
即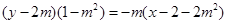
当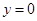 时得
时得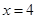
∴直线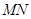 过定点(4,0). 14分
过定点(4,0). 14分
注:第(2)中的第(i)问:
S四边形ABCD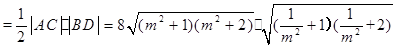
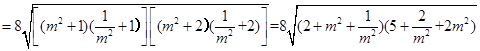
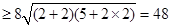 (当且仅当
(当且仅当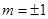 时取等号)也可.
时取等号)也可.
考点:本题主要考查抛物线标准方程,简单几何性质,直线与抛物线的位置关系,弦长公式,基本不等式,二次函数在闭区间上的最值问题等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
相关题目
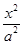 +
+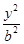 =1
=1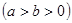 的离心率为
的离心率为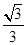 ,左焦点为F(-1,0),
,左焦点为F(-1,0),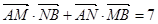 ,求直线L的方程;
,求直线L的方程;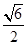 ?
?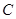 的离心率
的离心率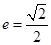 ,长轴的左右端点分别为
,长轴的左右端点分别为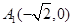 ,
,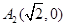 .
.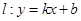 与曲线
与曲线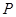 ,且与直线
,且与直线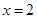 相交于点
相交于点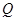 .
.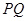 为直径的圆过定点
为直径的圆过定点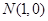 .
.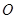 与直线
与直线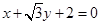 相切于点
相切于点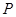 ,与
,与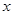 正半轴交于点
正半轴交于点 ,与直线
,与直线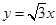 在第一象限的交点为
在第一象限的交点为 .点
.点 为圆
为圆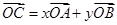 ,动点
,动点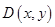 的轨迹记为曲线
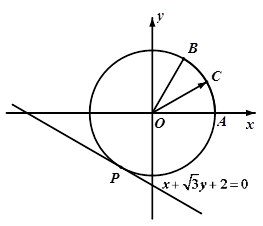
的轨迹记为曲线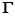 .
.
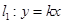 和
和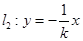 分别交曲线
分别交曲线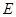 、
、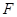 和
和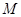 、
、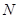 ,求四边形
,求四边形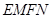 面积的最大值,并求此时的
面积的最大值,并求此时的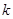 的值.
的值.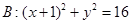 ,C为圆B上任意一点,求AC垂直平分线与线段BC的交点P的轨迹方程。
,C为圆B上任意一点,求AC垂直平分线与线段BC的交点P的轨迹方程。 的内切圆与三边
的内切圆与三边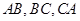 的切点分别为
的切点分别为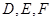 ,已知
,已知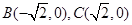 ,内切圆圆心
,内切圆圆心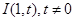 ,设点A的轨迹为R.
,设点A的轨迹为R. 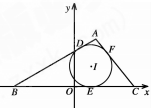
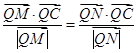 恒成立,若求出Q点的坐标,若不存在,说明理由.
恒成立,若求出Q点的坐标,若不存在,说明理由.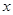 轴上的椭圆
轴上的椭圆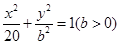 经过点
经过点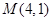 ,直线
,直线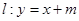
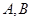 不同的两点.
不同的两点.
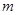 的取值范围;
的取值范围;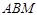 是以
是以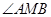 为直角的直角三角形,若存在,求出
为直角的直角三角形,若存在,求出 中,已知
中,已知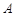 ,
,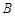 ,
, 是椭圆
是椭圆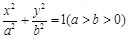 上不同的三点,
上不同的三点,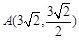 ,
,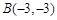 ,
,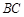 的中点在直线
的中点在直线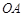 上.
上.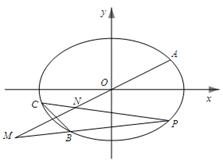
 在椭圆上(异于点
在椭圆上(异于点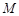 ,
,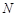 两点,证明
两点,证明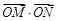 为定值并求出该定值.
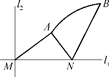
为定值并求出该定值.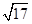 ,|AN|=3,且|NB|=6,建立适当的坐标系,求曲线段C的方程.
,|AN|=3,且|NB|=6,建立适当的坐标系,求曲线段C的方程.