题目内容
椭圆 (a>b>0)与x轴,y轴的正半辆分别交于A,B两点,原点O到直线AB的距离为
(a>b>0)与x轴,y轴的正半辆分别交于A,B两点,原点O到直线AB的距离为 ,该椭圆的离心率为
,该椭圆的离心率为 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点 的直线l与椭圆交于两个不同的点M,N,求线段MN的垂直平分线在y轴上截距的取值范围.
的直线l与椭圆交于两个不同的点M,N,求线段MN的垂直平分线在y轴上截距的取值范围.
解:(Ⅰ)设直线AB的方程为bx+ay-ab=0
∵原点O到直线AB的距离为 ,∴
,∴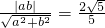 ①
①
∵椭圆的离心率为 ,∴
,∴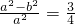 ②
②
由①②可得:a=2,b=1
∴椭圆的方程为 ;
;
(Ⅱ)当直线斜率不存在时,线段MN的垂直平分线的纵截距为0
当直线斜率k存在时,设直线l的方程为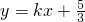 ,代入
,代入 ,消去y得(9+36k2)x2+120kx+64=0
,消去y得(9+36k2)x2+120kx+64=0
∵△=14400k2-256(9+36k2)>0,∴
设M(x1,y1),N(x2,y2),MN的中点为Q(x0,y0)
∴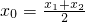 =
= ,
,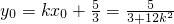
∴Q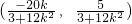
∴线段MN的垂直平分线方程为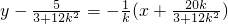
令x=0,则y= ,
,
由 ,可得-
,可得-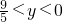
∴线段MN的垂直平分线在y轴上截距的取值范围为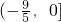 .
.
分析:(Ⅰ)设直线AB的方程为bx+ay-ab=0,利用原点O到直线AB的距离为 ,椭圆的离心率为
,椭圆的离心率为 ,建立方程可求a、b的值,从而可得椭圆的方程;
,建立方程可求a、b的值,从而可得椭圆的方程;
(Ⅱ)当直线斜率不存在时,线段MN的垂直平分线的纵截距为0;当直线斜率k存在时,设直线l的方程为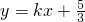 ,代入
,代入 ,消去y得(9+36k2)x2+120kx+64=0,进而可求线段MN的垂直平分线方程,由此即可求得线段MN的垂直平分线在y轴上截距的取值范围.
,消去y得(9+36k2)x2+120kx+64=0,进而可求线段MN的垂直平分线方程,由此即可求得线段MN的垂直平分线在y轴上截距的取值范围.
点评:本题综合考查椭圆的标准方程,考查直线与椭圆的位置关系,解题的关键是确定线段MN的垂直平分线.
∵原点O到直线AB的距离为
 ,∴
,∴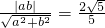 ①
①∵椭圆的离心率为
 ,∴
,∴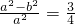 ②
②由①②可得:a=2,b=1
∴椭圆的方程为
 ;
;(Ⅱ)当直线斜率不存在时,线段MN的垂直平分线的纵截距为0
当直线斜率k存在时,设直线l的方程为
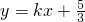 ,代入
,代入 ,消去y得(9+36k2)x2+120kx+64=0
,消去y得(9+36k2)x2+120kx+64=0∵△=14400k2-256(9+36k2)>0,∴

设M(x1,y1),N(x2,y2),MN的中点为Q(x0,y0)
∴
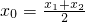 =
= ,
,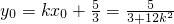
∴Q
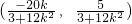
∴线段MN的垂直平分线方程为
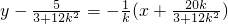
令x=0,则y=
 ,
,由
 ,可得-
,可得-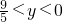
∴线段MN的垂直平分线在y轴上截距的取值范围为
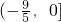 .
.分析:(Ⅰ)设直线AB的方程为bx+ay-ab=0,利用原点O到直线AB的距离为
 ,椭圆的离心率为
,椭圆的离心率为 ,建立方程可求a、b的值,从而可得椭圆的方程;
,建立方程可求a、b的值,从而可得椭圆的方程;(Ⅱ)当直线斜率不存在时,线段MN的垂直平分线的纵截距为0;当直线斜率k存在时,设直线l的方程为
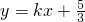 ,代入
,代入 ,消去y得(9+36k2)x2+120kx+64=0,进而可求线段MN的垂直平分线方程,由此即可求得线段MN的垂直平分线在y轴上截距的取值范围.
,消去y得(9+36k2)x2+120kx+64=0,进而可求线段MN的垂直平分线方程,由此即可求得线段MN的垂直平分线在y轴上截距的取值范围.点评:本题综合考查椭圆的标准方程,考查直线与椭圆的位置关系,解题的关键是确定线段MN的垂直平分线.

练习册系列答案
相关题目
 (a>b>0)与双曲线
(a>b>0)与双曲线 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于
有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于 两点.若C1恰好将线段
两点.若C1恰好将线段 三等分,则
三等分,则 (B)a2=13 (C)b2=
(B)a2=13 (C)b2= (D)b2=2
(D)b2=2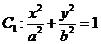 (a>b>0)与双曲线
(a>b>0)与双曲线 有公共的焦点,C2的一条渐近线与C1C2的长度为直径的圆相交于
有公共的焦点,C2的一条渐近线与C1C2的长度为直径的圆相交于 两点.若C1恰好将线段
两点.若C1恰好将线段 三等分,则
三等分,则 (B)a2=13
(C)b2=
(B)a2=13
(C)b2= (D)b2=2
(D)b2=2 (a>b>0)与双曲线
(a>b>0)与双曲线 (m>0,n>0)有相同的焦点(-c,0)和(c,0),若c是a、m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率是 ( )
(m>0,n>0)有相同的焦点(-c,0)和(c,0),若c是a、m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率是 ( )  B.
B. 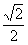 C.
C.  D.
D. 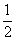
 (a>b>0)与直线x+y=1交于P、Q两点,且OP⊥OQ,其中O为坐标原点.
(a>b>0)与直线x+y=1交于P、Q两点,且OP⊥OQ,其中O为坐标原点. 的值;
的值; ≤e≤
≤e≤ ,求椭圆长轴的取值范围.
,求椭圆长轴的取值范围. (a>b>0)与圆
(a>b>0)与圆 (c为椭圆半焦距)有四个不同交点,则离心率的取值范围是( )
(c为椭圆半焦距)有四个不同交点,则离心率的取值范围是( )


