题目内容
已知椭圆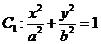 (a>b>0)与双曲线
(a>b>0)与双曲线 有公共的焦点,C2的一条渐近线与C1C2的长度为直径的圆相交于
有公共的焦点,C2的一条渐近线与C1C2的长度为直径的圆相交于 两点.若C1恰好将线段
两点.若C1恰好将线段 三等分,则
三等分,则
(A)a2 = (B)a2=13
(C)b2=
(B)a2=13
(C)b2= (D)b2=2
(D)b2=2
【答案】
C
【解析】由双曲线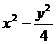 =1知渐近线方程为
=1知渐近线方程为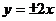 ,又∵椭圆与双曲线有公共焦点,
,又∵椭圆与双曲线有公共焦点,
∴椭圆方程可化为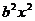 +
+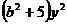 =
=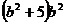 ,联立直线与椭圆方程消
,联立直线与椭圆方程消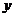 得,
得,
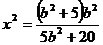 ,又∵
,又∵ 将线段AB三等分,∴
将线段AB三等分,∴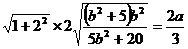 ,
,
解之得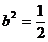 .
.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
 =2
=2 ,
, ·
· =
= ,求椭圆的方程.
,求椭圆的方程. (a>b>0),点
(a>b>0),点 在椭圆上。
在椭圆上。 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B. 分)
分) (a>b>0)的离心率
(a>b>0)的离心率 ,焦距是函数
,焦距是函数 的零点.
的零点. 与椭圆交于
与椭圆交于 、
、 两点,
两点, ,求k的值.
,求k的值.