题目内容
椭圆 (a>b>0)与圆
(a>b>0)与圆 (c为椭圆半焦距)有四个不同交点,则离心率的取值范围是( )
(c为椭圆半焦距)有四个不同交点,则离心率的取值范围是( )A.

B.

C.

D.

【答案】分析:联立椭圆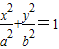 (a>b>0)与圆
(a>b>0)与圆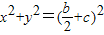 ,消去y2,可得
,消去y2,可得 ,根据椭圆
,根据椭圆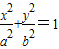 (a>b>0)与圆
(a>b>0)与圆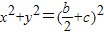 (c为椭圆半焦距)有四个不同交点,可知方程有两个不等的根,结合椭圆的范围,即可求得离心率的取值范围.
(c为椭圆半焦距)有四个不同交点,可知方程有两个不等的根,结合椭圆的范围,即可求得离心率的取值范围.
解答:解:联立椭圆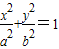 (a>b>0)与圆
(a>b>0)与圆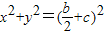 ,消去y2,可得
,消去y2,可得
∵椭圆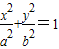 (a>b>0)与圆
(a>b>0)与圆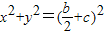 (c为椭圆半焦距)有四个不同交点,
(c为椭圆半焦距)有四个不同交点,
∴0<x2<a2
∴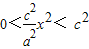
∴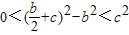
∴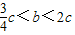
∴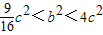
∴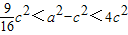
∴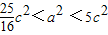
∴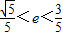
故选A.
点评:本题考查的重点是椭圆的几何性质,解题的关键是将椭圆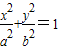 (a>b>0)与圆
(a>b>0)与圆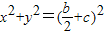 (c为椭圆半焦距)联立,利用有四个不同交点,结合0<x2<a2,从而使问题得解,综合性强.
(c为椭圆半焦距)联立,利用有四个不同交点,结合0<x2<a2,从而使问题得解,综合性强.
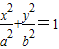 (a>b>0)与圆
(a>b>0)与圆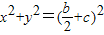 ,消去y2,可得
,消去y2,可得 ,根据椭圆
,根据椭圆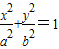 (a>b>0)与圆
(a>b>0)与圆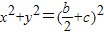 (c为椭圆半焦距)有四个不同交点,可知方程有两个不等的根,结合椭圆的范围,即可求得离心率的取值范围.
(c为椭圆半焦距)有四个不同交点,可知方程有两个不等的根,结合椭圆的范围,即可求得离心率的取值范围.解答:解:联立椭圆
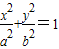 (a>b>0)与圆
(a>b>0)与圆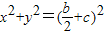 ,消去y2,可得
,消去y2,可得
∵椭圆
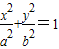 (a>b>0)与圆
(a>b>0)与圆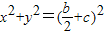 (c为椭圆半焦距)有四个不同交点,
(c为椭圆半焦距)有四个不同交点,∴0<x2<a2
∴
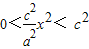
∴
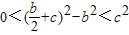
∴
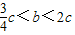
∴
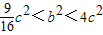
∴
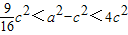
∴
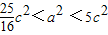
∴
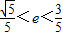
故选A.
点评:本题考查的重点是椭圆的几何性质,解题的关键是将椭圆
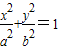 (a>b>0)与圆
(a>b>0)与圆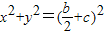 (c为椭圆半焦距)联立,利用有四个不同交点,结合0<x2<a2,从而使问题得解,综合性强.
(c为椭圆半焦距)联立,利用有四个不同交点,结合0<x2<a2,从而使问题得解,综合性强. 
练习册系列答案
相关题目
 (a>b>0)与双曲线
(a>b>0)与双曲线 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于
有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于 两点.若C1恰好将线段
两点.若C1恰好将线段 三等分,则
三等分,则 (B)a2=13 (C)b2=
(B)a2=13 (C)b2= (D)b2=2
(D)b2=2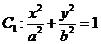 (a>b>0)与双曲线
(a>b>0)与双曲线 有公共的焦点,C2的一条渐近线与C1C2的长度为直径的圆相交于
有公共的焦点,C2的一条渐近线与C1C2的长度为直径的圆相交于 两点.若C1恰好将线段
两点.若C1恰好将线段 三等分,则
三等分,则 (B)a2=13
(C)b2=
(B)a2=13
(C)b2= (D)b2=2
(D)b2=2 (a>b>0)与双曲线
(a>b>0)与双曲线 (m>0,n>0)有相同的焦点(-c,0)和(c,0),若c是a、m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率是 ( )
(m>0,n>0)有相同的焦点(-c,0)和(c,0),若c是a、m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率是 ( )  B.
B. 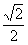 C.
C.  D.
D. 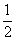
 (a>b>0)与直线x+y=1交于P、Q两点,且OP⊥OQ,其中O为坐标原点.
(a>b>0)与直线x+y=1交于P、Q两点,且OP⊥OQ,其中O为坐标原点. 的值;
的值; ≤e≤
≤e≤ ,求椭圆长轴的取值范围.
,求椭圆长轴的取值范围.