题目内容
椭圆 (a>b>0)与直线x+y=1交于P、Q两点,且OP⊥OQ,其中O为坐标原点.
(a>b>0)与直线x+y=1交于P、Q两点,且OP⊥OQ,其中O为坐标原点.(1)求
 的值;
的值;(2)若椭圆的离心率e满足
 ≤e≤
≤e≤ ,求椭圆长轴的取值范围.
,求椭圆长轴的取值范围.
【答案】分析:(1)设P(x1,y1),Q(x2,y2)由OP⊥OQ 可得 x 1x 2+y1 y 2=0结合y1=1-x1,y2=1-x2可得2x1x2-(x1+x2)+1=0,将y=1-x代入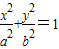 可得(a2+b2)x2-2a2x+a2(1-b2)=0则
可得(a2+b2)x2-2a2x+a2(1-b2)=0则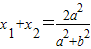 ,
,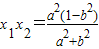 代入整理可求
代入整理可求
(2))由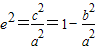 及
及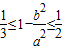 ,
,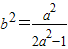 可求a得范围
可求a得范围
解答:解:设P(x1,y1),Q(x2,y2)由OP⊥OQ 可得 x 1x 2+y1 y 2=0(2分)
∵y1=1-x1,y2=1-x2
∴2x1x2-(x1+x2)+1=0①又将y=1-x代入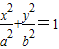 可得(a2+b2)x2-2a2x+a2(1-b2)=0
可得(a2+b2)x2-2a2x+a2(1-b2)=0
∵△>0∴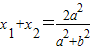 ,
,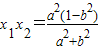 (4分)
(4分)
代入①化简得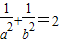 .(6分)
.(6分)
(2)∵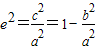
∴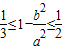
∴ (8分)
(8分)
又由(1)知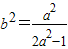 (9分)
(9分)
∴ ∴
∴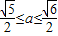 ,(11分)
,(11分)
∴长轴 2a∈[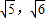 ].(12分)
].(12分)
点评:本题主要考查了直线与圆锥曲线的位置关系的应用,方程的思想的应用圆锥曲线的性质的应用,属于性质的应用,要求具备一定的综合应用知识的能力.
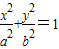 可得(a2+b2)x2-2a2x+a2(1-b2)=0则
可得(a2+b2)x2-2a2x+a2(1-b2)=0则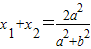 ,
,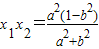 代入整理可求
代入整理可求(2))由
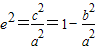 及
及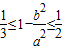 ,
,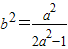 可求a得范围
可求a得范围解答:解:设P(x1,y1),Q(x2,y2)由OP⊥OQ 可得 x 1x 2+y1 y 2=0(2分)
∵y1=1-x1,y2=1-x2
∴2x1x2-(x1+x2)+1=0①又将y=1-x代入
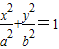 可得(a2+b2)x2-2a2x+a2(1-b2)=0
可得(a2+b2)x2-2a2x+a2(1-b2)=0∵△>0∴
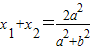 ,
,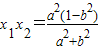 (4分)
(4分)代入①化简得
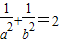 .(6分)
.(6分)(2)∵
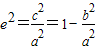
∴
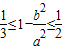
∴
 (8分)
(8分)又由(1)知
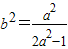 (9分)
(9分)∴
 ∴
∴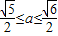 ,(11分)
,(11分)∴长轴 2a∈[
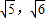 ].(12分)
].(12分)点评:本题主要考查了直线与圆锥曲线的位置关系的应用,方程的思想的应用圆锥曲线的性质的应用,属于性质的应用,要求具备一定的综合应用知识的能力.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 (a>b>0)与双曲线
(a>b>0)与双曲线 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于
有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于 两点.若C1恰好将线段
两点.若C1恰好将线段 三等分,则
三等分,则 (B)a2=13 (C)b2=
(B)a2=13 (C)b2= (D)b2=2
(D)b2=2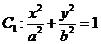 (a>b>0)与双曲线
(a>b>0)与双曲线 有公共的焦点,C2的一条渐近线与C1C2的长度为直径的圆相交于
有公共的焦点,C2的一条渐近线与C1C2的长度为直径的圆相交于 两点.若C1恰好将线段
两点.若C1恰好将线段 三等分,则
三等分,则 (B)a2=13
(C)b2=
(B)a2=13
(C)b2= (D)b2=2
(D)b2=2 (a>b>0)与双曲线
(a>b>0)与双曲线 (m>0,n>0)有相同的焦点(-c,0)和(c,0),若c是a、m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率是 ( )
(m>0,n>0)有相同的焦点(-c,0)和(c,0),若c是a、m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率是 ( )  B.
B. 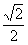 C.
C.  D.
D. 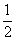
 (a>b>0)与圆
(a>b>0)与圆 (c为椭圆半焦距)有四个不同交点,则离心率的取值范围是( )
(c为椭圆半焦距)有四个不同交点,则离心率的取值范围是( )


