题目内容
16.设$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$为一组基底,$\overrightarrow{OA}$=-2$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$,$\overrightarrow{OB}$=m$\overrightarrow{{e}_{2}}$,$\overrightarrow{OC}$=n$\overrightarrow{{e}_{1}}$,如果A、B、C三点共线,则$\frac{1}{m}$+$\frac{1}{n}$=-$\frac{1}{2}$.分析 根据三点共线的条件,建立方程$\overrightarrow{AB}$=t$\overrightarrow{AB}$,利用向量共线的基本定理进行求解即可.
解答 解:∵$\overrightarrow{OA}$=-2$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$,$\overrightarrow{OB}$=m$\overrightarrow{{e}_{2}}$,$\overrightarrow{OC}$=n$\overrightarrow{{e}_{1}}$,
∴$\overrightarrow{AB}$=$\overrightarrow{OB}$-$\overrightarrow{OA}$=m$\overrightarrow{{e}_{2}}$-(-2$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$)=2$\overrightarrow{{e}_{1}}$+(m+2)$\overrightarrow{{e}_{2}}$,
$\overrightarrow{AC}$=$\overrightarrow{OC}$-$\overrightarrow{OA}$=n$\overrightarrow{{e}_{1}}$-(-2$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$)=(2+n)$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$,
若A、B、C三点共线,
则存在一个常数t,
有$\overrightarrow{AB}$=t$\overrightarrow{AC}$,
即2$\overrightarrow{{e}_{1}}$+(m+2)$\overrightarrow{{e}_{2}}$=t((2+n)$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$),
则$\left\{\begin{array}{l}{2=(2+n)t}\\{m+2=2t}\end{array}\right.$,消去参数t得4t=(n+2)(m+2)t,
即4=(n+2)(m+2),
则mn+2(m+n)=0,
则mn=-2(m+n),
即1=-2($\frac{1}{m}$+$\frac{1}{n}$),
则$\frac{1}{m}$+$\frac{1}{n}$=-$\frac{1}{2}$,
故答案为:-$\frac{1}{2}$.
点评 本题主要考查三点共线的应用,结合向量共线的基本定理建立方程关系是解决本题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 非p且q | B. | p且q | C. | p且非q | D. | 非p且非q |
| A. | ∅ | B. | R | C. | {x|x≠-$\frac{b}{2a}$} | D. | 与a的正负有关 |
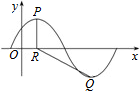 已知函数f(x)=Asin($\frac{π}{3}$x+φ),(A>0,0<φ<$\frac{π}{2}$),y=f(x)的部分图象如图所示,P,Q分别为该图象上相邻的最高点和最低点,点P在x轴上的射影为R(1,0),cos∠PRQ=-$\frac{4}{5}$
已知函数f(x)=Asin($\frac{π}{3}$x+φ),(A>0,0<φ<$\frac{π}{2}$),y=f(x)的部分图象如图所示,P,Q分别为该图象上相邻的最高点和最低点,点P在x轴上的射影为R(1,0),cos∠PRQ=-$\frac{4}{5}$