题目内容
【题目】已知等差数列{an}中,a1=1,且a2+2,a3 , a4﹣2成等比数列.
(1)求数列{an}的通项公式;
(2)若bn= ![]() ,求数列{bn}的前n项和Sn .
,求数列{bn}的前n项和Sn .
【答案】
(1)解:由a2+2,a3,a4﹣2成等比数列,
∴ ![]() =(a2+2)(a4﹣2),
=(a2+2)(a4﹣2),
(1+2d)2=(3+d)(﹣1+3d),
d2﹣4d+4=0,解得:d=2,
∴an=1+2(n﹣1)=2n﹣1,
数列{an}的通项公式an=2n﹣1
(2)解:bn= ![]() =
= ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),
),
Sn= ![]() [(1﹣
[(1﹣ ![]() )+(
)+( ![]() ﹣
﹣ ![]() )+…+(
)+…+( ![]() ﹣
﹣ ![]() )],
)],
= ![]() (1﹣
(1﹣ ![]() ),
),
= ![]() ,
,
数列{bn}的前n项和Sn,Sn= ![]()
【解析】(1)由a2+2,a3 , a4﹣2成等比数列, ![]() =(a2+2)(a4﹣2),根据等差数列的通项公式求得d2﹣4d+4=0,即可求得d=2,数列{an}的通项公式;(2)bn=
=(a2+2)(a4﹣2),根据等差数列的通项公式求得d2﹣4d+4=0,即可求得d=2,数列{an}的通项公式;(2)bn= ![]() =
= ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),利用“裂项法”即可求得数列{bn}的前n项和Sn .
),利用“裂项法”即可求得数列{bn}的前n项和Sn .
【考点精析】根据题目的已知条件,利用数列的前n项和的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系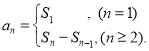 .
.

练习册系列答案
相关题目
【题目】某特色餐馆开通了美团外卖服务,在一周内的某特色菜外卖份数![]() (份)与收入
(份)与收入![]() (元)之间有如下的对应数据:
(元)之间有如下的对应数据:
外卖份数 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |
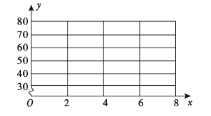
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计外卖份数为12份时,收入为多少元.
注:①参考公式:线性回归方程系数公式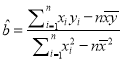 ,
, ![]() ;
;
②参考数据: ![]() ,
, ![]() ,
, ![]() .
.