题目内容
【题目】已知函数![]() .
.
(1)若![]() ,试判断
,试判断![]() 的符号;
的符号;
(2)讨论![]() 的零点的个数.
的零点的个数.
【答案】(1)答案不唯一,具体见解析(2)当![]() 或
或![]() 时,
时,![]() 有
有![]() 个零点;当
个零点;当![]() 且
且![]() 时,
时,![]() 有
有![]() 个零点
个零点
【解析】
(1)首先计算得到![]() ,设
,设![]() ,利用二次求导,判断函数的单调性,
,利用二次求导,判断函数的单调性,![]() 和
和![]() 比较大小;
比较大小;
(2)首先求函数的导数![]() ,讨论
,讨论![]() ,
,![]() 两种情况讨论函数的单调性,判断函数的零点个数,当
两种情况讨论函数的单调性,判断函数的零点个数,当![]() 时,
时,![]() ,
,
设![]() ,再次求函数的导数,判断函数的单调性和最小值,讨论求函数的零点个数.
,再次求函数的导数,判断函数的单调性和最小值,讨论求函数的零点个数.
解:(1)![]() .
.
设![]() ,则
,则![]() .
.
设![]() ,则
,则![]() ,
,
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
∴当![]() 时,
时,![]() .故
.故![]() ,从而
,从而![]() .
.
∴![]() 在
在![]() 上单调递增.
上单调递增.
∴当![]() 时,
时,![]() ,从而
,从而![]() ;
;
当![]() 时,
时,![]() ,从而
,从而![]() ;
;
当![]() 时,
时,![]() ,从而
,从而![]() .
.
(2)![]() 的定义域为
的定义域为![]() ,
,![]() .
.
∴当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,∴
,∴![]() 有
有![]() 个零点.
个零点.
当![]() 时,令
时,令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() .
.
∴![]() 在上
在上![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
∴![]() .
.
设![]() ,则
,则![]() .
.
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .∴
.∴![]() .
.
∴当![]() 时,
时,![]() ,即
,即![]() ,
,
又当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;故
;故![]() 有
有![]() 个零点.
个零点.
当![]() 时,
时,![]() ,故
,故![]() 有
有![]() 个零点.
个零点.
当![]() 时,
时,![]() ,即
,即![]() ,
,
又当![]() 时,
时,![]() ;由(1)知
;由(1)知![]() ,故
,故![]() 有
有![]() 个零点.
个零点.
当![]() 或
或![]() 时,
时,![]() 有
有![]() 个零点;当
个零点;当![]() 且
且![]() 时,
时,![]() 有
有![]() 个零点.
个零点.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
【题目】某企业为确定下一年度投入某种产品的生产所需的资金,需了解每投入2千万资金后,工人人数![]() (单位:百人)对年产能
(单位:百人)对年产能![]() (单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.
(单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
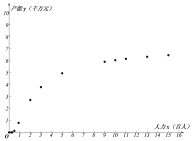
(1)根据散点图判断:![]() 与
与![]() 哪一个适宜作为年产能
哪一个适宜作为年产能![]() 关于投入的人力
关于投入的人力![]() 的回归方程类型?并说明理由?
的回归方程类型?并说明理由?
(2)根据(1)的判断结果及相关的计算数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)现该企业共有2000名生产工人,资金非常充足,为了使得年产能达到最大值,则下一年度共需投入多少资金(单位:千万元)?
附注:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为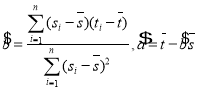 ,(说明:
,(说明:![]() 的导函数为
的导函数为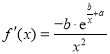 )
)