题目内容
2.已知圆锥的侧面积为15πcm2,底面半径为3cm,则圆锥的高是( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 8cm |
分析 由圆锥的侧面积公式,先求出圆锥的母线长,进而可得圆锥的高.
解答 解:∵圆锥的侧面积为15πcm2,底面半径为3cm,
∴圆锥的母线长满足:3πl=15πcm2,解得:l=5cm,
∴圆锥的高h=$\sqrt{{l}^{2}-{r}^{2}}$=4cm,
故选:B.
点评 本题考查的知识点是旋转体,熟练掌握圆锥的侧面积公式及圆锥的几何特征,是解答的关键.

练习册系列答案
相关题目
12.设向量$\vec a=(1,\;x)$,$\vec b=(x,4)$,则$x=\int_0^{\sqrt{2}}{2tdt}$是$\vec a$∥$\vec b$的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 即不充分也不必要 |
13.已知矩形ABCD中,$AB=\sqrt{2}$,BC=1,则$\overrightarrow{AC}•\overrightarrow{DB}$=( )
| A. | 1 | B. | -1 | C. | $\sqrt{6}$ | D. | $2\sqrt{2}$ |
7.设f(x)=lg$\frac{1+{2}^{x}+{3}^{x}+…+9{9}^{x}+a•10{0}^{x}}{100}$,其中a是实数,如果f(x)当x∈(-∞,1]时有意义,求a的取值范围.
11.设复数z=1+i(i是虚数单位),则复数z+$\frac{1}{z}$的虚部是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2}$i | C. | $\frac{3}{2}$ | D. | $\frac{3}{2}$i |
12.如图,给出事件A与B的关系示意图,则( )
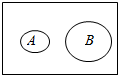

| A. | A⊆B | B. | A与B互斥 | ||
| C. | B⊆A | D. | A与B互为对立事件 |