题目内容
已知数列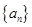 满足:
满足: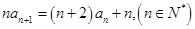 且
且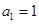 .
.
(1)求数列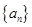 的通项公式;
的通项公式;
(2)令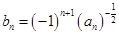 ,数列
,数列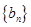 的前项和为
的前项和为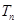 ,求证:
,求证: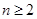 时,
时,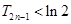 且
且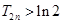
(1)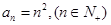 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)由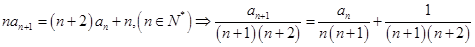
令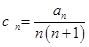 ,然后用迭加法求出数列
,然后用迭加法求出数列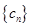 的通项公式,最后求数列
的通项公式,最后求数列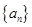 的通项公式;
的通项公式;
(2)由(1)知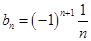 ,写出
,写出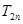 及
及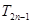 并化简,利用函数的思想解决与数列有关的不等式问题.
并化简,利用函数的思想解决与数列有关的不等式问题.
解:(1)易知: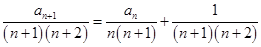 ,
,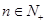
令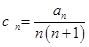 得,
得,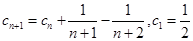
若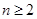 ,则
,则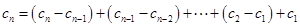
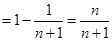
当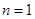 时,
时, 也满足上式,故
也满足上式,故
所以 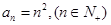 6分
6分
(2)易知: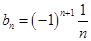
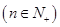
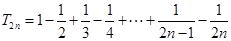

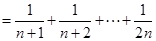
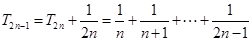 8分
8分
先证不等式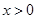 时,
时,
令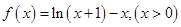 ,则
,则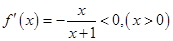
∴ 在
在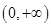 上单调递减,即
上单调递减,即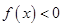
同理:令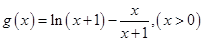 ,则
,则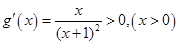
∴ 在
在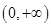 上单调递增,即
上单调递增,即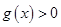 ,得证.
,得证.
取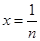 ,得
,得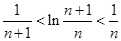 ,所以
,所以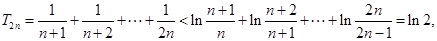
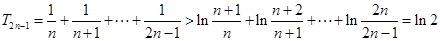 14分
14分
考点:1、数列的递推公式;2、函数思想在数列综合问题中的应用.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
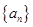 中,
中,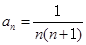 ,其前n项的和是
,其前n项的和是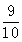 ,则在平面直角坐标系中,直线
,则在平面直角坐标系中,直线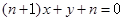 在y轴上的截距为 。
在y轴上的截距为 。 的前n项和记为
的前n项和记为 ,点(n,
,点(n,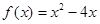 (
(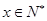 )上
)上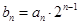 ,求数列
,求数列 的前n项和
的前n项和 的值.
的值.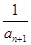 +
+ +
+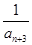 +…+
+…+ ,若对任意的正整数n,当m∈[-1,1]时,不等式t2-2mt+
,若对任意的正整数n,当m∈[-1,1]时,不等式t2-2mt+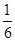 >bn恒成立,求实数t的取值范围.
>bn恒成立,求实数t的取值范围.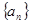 的各项均为正数,且
的各项均为正数,且
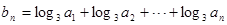 ,求数列
,求数列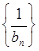 的前n项和
的前n项和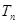 ;
;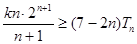 恒成立的实数
恒成立的实数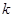 的取值范围.
的取值范围.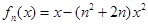 (其中
(其中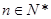 ),区间
),区间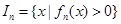 .
. 的长度(注:区间
的长度(注:区间 的长度定义为
的长度定义为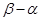 );
);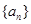 ,令
,令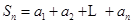 ,证明:
,证明: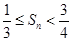 .
. 的前
的前 项和为
项和为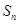 ,
,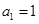 ,
,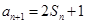 ,等差数列
,等差数列 满足
满足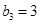 ,
,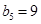 .
.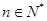 ,不等式
,不等式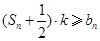 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.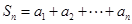 ,
, ,且
,且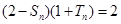 ,
, .
.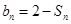 ,证明数列{bn}是等比数列;
,证明数列{bn}是等比数列;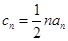 ,求集合
,求集合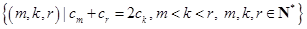 .
.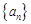 的前
的前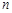 项和
项和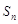 满足
满足 ,又
,又 ,
,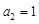 .
.