题目内容
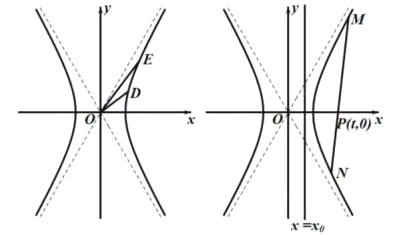
【题目】设F1 ， F2为双曲线C： 
的左，右焦点，P，Q为双曲线C右支上的两点，若 
=2 
，且 
=0，则该双曲线的离心率是（ ）
A.
B.2
C.
D.
【答案】C
【解析】解：∵经过右焦点F2的直线与双曲线C的右支交于P，Q两点，且|PF2|=2|F2Q|， ∴设|F2Q|=m，则|PF2|=2|F2Q|=2m，
|PF1|=|PF2|+2a=2m+2a，
|QF1|=|QF2|+2a=m+2a，
∵PQ⊥F1Q，
∴|PF1|2=|PQ|2+|QF1|2 ，
即（2m+2a）2=（3m）2+（m+2a）2 ，
整理得4m2+8ma+4a2=9m2+m2+8ma+4a2 ，
即4am=6m2 ，
则m= 
a，
则|QF1|= a+2a= 
，|F2Q|= a，
由|F1F2|2=|F1Q|2+|QF2|2 ，
即4c2=（ ）2+（ a）2= 
，
则e= 
= 
，
故选：C．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
【题目】某商场举行有奖促销活动，顾客购买一定金额的商品后即可参加一次抽奖.随着抽奖活动的有效开展，参与抽奖活动的人数越来越多，该商场对前5天抽奖活动的人数进行统计，y表示第x天参加抽奖活动的人数，得到统计表如下：
x | 1 | 2 | 3 | 4 | 5 |
y | 50 | 60 | 70 | 80 | 100 |
经过进一步统计分析，发现y与x具有线性相关关系.
（1）若从这5天随机抽取两天，求至少有1天参加抽奖人数超过70的概率；
（2）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
，并估计该活动持续7天，共有多少名顾客参加抽奖？
参考公式及数据：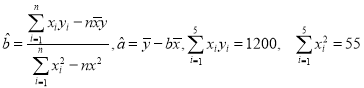
.
