题目内容
15．若函数f（x）在它的定义域（0，+∞）内为增函数，且对任意正数x，都有f（f（x）-lnx）=1，e是自然对数的底数，则f（e）的值等于（ ）| A． | 1 | B． | 2 | C． | e | D． | e+1 |
分析 利用换元法 将函数转化为f（x）=lnx+t，根据函数的对应关系求出t的值，即可求出函数f（x）的表达式，即可得到结论．
解答 解：设t=f（x）-lnx，
则f（x）=lnx+t，则条件等价为f（t）=1，
令x=t，则f（t）=lnt+t=1，
函数f（x）在它的定义域（0，+∞）内为增函数，
∴函数为一对一函数，解得t=1，
∴f（x）=lnx+1，
则f（e）=1+1=2，
故选：B．
点评 本题主要考查函数值的计算，利用换元法求出函数的解析式是解决本题的关键．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
20．下列说法中，正确的是（ ）
| A． | 集合{x|x∈Z，|x|＜2}的非空真子集的个数是7 | |
| B． | 函数y=（$\frac{1}{2}$）${\;}^{{x}^{2}-3x+2}$的单调递减区间是（-∞，$\frac{3}{2}$] | |
| C． | 已知函数f（x）是定义在R上的奇函数，当x∈（-∞，0）时，f（x）=x-x4，则当x∈（0，+∞）时，f（x）=-x-x4 | |
| D． | 已知f（$\frac{2}{x}$+1）=x+3，则f（x）=$\frac{3x-1}{x-1}$ |
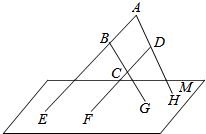如图，四边形ABCD中，AB∥DC，AB，BC，DC，AD（或其延长线）分别与平面M相交于E，F，G，H，求证：E，F，G，H必在同一直线上．