题目内容
16.对于函数y=f(x),若存在x0∈D使得f(-x0)+f(x0)=0则称函数f(x)为“次奇函数”且x0为该函数的一个“次奇点”,给出下列命题:①奇函数必为“次奇函数”;
②存在某个偶函数,它是“次奇函数”;
③若函数$f(x)=sin(x+\frac{π}{5})$为“次奇函数”,则该函数的所有“次奇点”为$\frac{kπ}{2}(k∈Z)$;
④若函数$f(x)=lg\frac{a+x}{1-x}$为“次奇函数”,则a=±1
⑤若函数f(x)=4x-m•2x+1为“次奇函数”,则$m≥\frac{1}{2}$.其中的正确命题是①②④⑤(写出你认为正确的所有命题的序号)
分析 根据已知中若存在x0∈D使得f(-x0)+f(x0)=0则称函数f(x)为“次奇函数”且x0为该函数的一个“次奇点”,逐一分析五个结论的真假,可得答案.
解答 解:①奇函数f(x)中,当x0∈D时,f(-x0)+f(x0)=0恒成立,故必为“次奇函数”,故①正确;
②存偶函数f(x)=|x|-1,易得当x0=±1时,使得f(-x0)+f(x0)=0,它是“次奇函数”,故②正确;
③若函数$f(x)=sin(x+\frac{π}{5})$为“次奇函数”,则$sin(-x+\frac{π}{5})+sin(x+\frac{π}{5})$=0有解:
则$sin(x-\frac{π}{5})=sin(x+\frac{π}{5})$有解,则由$(x-\frac{π}{5})-(x+\frac{π}{5})$=-$\frac{2π}{5}$得:$(x-\frac{π}{5})+(x+\frac{π}{5})=2kπ+π,k∈Z$,
解得:x=kπ+$\frac{π}{2}$,(k∈Z),即则该函数的所有“次奇点”为kπ+$\frac{π}{2}$,(k∈Z),故③错误;
④若函数$f(x)=lg\frac{a+x}{1-x}$为“次奇函数”,则$lg\frac{a-x}{1+x}+lg\frac{a+x}{1-x}$=0有解:
则$\frac{{a}^{2}-{x}^{2}}{1-{x}^{2}}=1$,则a=±1,故④正确;
⑤若函数f(x)=4x-m•2x+1为“次奇函数”,则4-x-m•2-x+1+4x-m•2x+1=0有解:
令t=2-x+2x,(t≥2),则t2-2mt-2=0有不小于2的根,
即m+$\sqrt{{m}^{2}+2}$≥2,解得:则$m≥\frac{1}{2}$,故⑤正确;
故正确的命题的序号是:①②④⑤,
故答案为:①②④⑤
点评 本题考查的知识点是命题的真假判断与应用,此类题型往往综合较多的其它知识点,综合性强,难度中档.

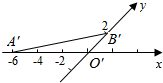 如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积是( )
如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积是( )| A. | 6 | B. | 3$\sqrt{2}$ | C. | 6$\sqrt{2}$ | D. | 12 |