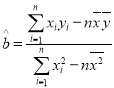ЬтФПФкШн
ЁОЬтФПЁПЮЊЙсГЙТфЪЕЕГжабыШЋУцНЈЩшаЁПЕЩчЛсЕФеНТдВПЪ№ЃЌФГЦЖРЇЕиЧјЕФЙуДѓЕГдБИЩВПЩюШыХЉДхЛ§МЋПЊеЙЁАОЋзМЗіЦЖЁБЙЄзї.ОЙ§ЖрФъЕФОЋаФАяЗіЃЌНижС2018ФъЕзЃЌАДееХЉДхМвЭЅШЫОљФъДПЪеШы8000дЊЕФаЁПЕБъзМЃЌИУЕиЧјНіЪЃВПЗжМвЭЅЩаЮДЪЕЯжаЁПЕ.ЯжДгетаЉЩаЮДЪЕЯжаЁПЕЕФМвЭЅжаЫцЛњГщШЁ50ЛЇЃЌЕУЕНет50ЛЇМвЭЅ2018ФъЕФМвЭЅШЫОљФъДПЪеШыЕФЦЕТЪЗжВМжБЗНЭМЃЌШчЭМ.
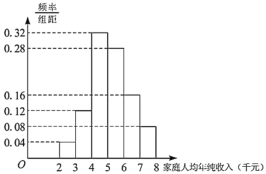
зЂЃКдкЦЕТЪЗжВМжБЗНЭМжаЃЌЭЌвЛзщЪ§ОнгУИУЧјМфЕФжаЕужЕзїДњБэ.
ЃЈ1ЃЉЙРМЦИУЕиЧјЩаЮДЪЕЯжаЁПЕЕФМвЭЅ2018ФъМвЭЅШЫОљФъДПЪеШыЕФЦНОљжЕЃЛ
ЃЈ2ЃЉ2019Фъ7дТЃЌЮЊЙРМЦИУЕиФмЗёдк2020ФъШЋУцЪЕЯжаЁПЕЃЌЪеМЏСЫЕБЕизюЦЖРЇЕФвЛЛЇМвЭЅ2019Фъ1жС6дТЕФШЫОљдТДПЪеШыЕФЪ§ОнЃЌзїГіЩЂЕуЭМШчЯТ.
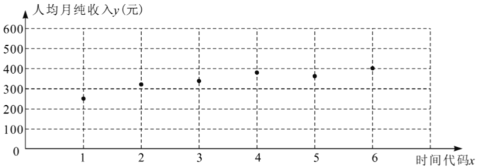
ИљОнЯрЙиадЗжЮіЃЌЗЂЯжЦфМвЭЅШЫОљдТДПЪеШы![]() гыЪБМфДњТы
гыЪБМфДњТы![]() жЎМфОпгаНЯЧПЕФЯпадЯрЙиЙиЯЕЃЈМЧ2019Фъ1дТЁЂ2дТЁЁЗжБ№ЮЊ
жЎМфОпгаНЯЧПЕФЯпадЯрЙиЙиЯЕЃЈМЧ2019Фъ1дТЁЂ2дТЁЁЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌвРДЫРрЭЦЃЉ.ЪддЄВтИУМвЭЅФмЗёдк2020ФъЪЕЯжаЁПЕЩњЛю.
ЃЌЁЃЌвРДЫРрЭЦЃЉ.ЪддЄВтИУМвЭЅФмЗёдк2020ФъЪЕЯжаЁПЕЩњЛю.
ВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() .
.
ВЮПМЙЋЪНЃКЯпадЛиЙщЗНГЬ![]() жаЃЌ
жаЃЌ ЃЌ
ЃЌ![]() .
.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈдЊЃЉЃЈ2ЃЉдЄВтИУМвЭЅФмдк2020ФъЪЕЯжаЁПЕЩњЛю
ЃЈдЊЃЉЃЈ2ЃЉдЄВтИУМвЭЅФмдк2020ФъЪЕЯжаЁПЕЩњЛю
ЁОНтЮіЁП
ЃЈ1ЃЉжБНгМЦЫуЕУЕНД№АИ.
ЃЈ2ЃЉМЦЫу![]() ЃЌ
ЃЌ![]() ЃЌЕУЕНЛиЙщЗНГЬ
ЃЌЕУЕНЛиЙщЗНГЬ![]() ЃЌШЁ
ЃЌШЁ![]() ЃЌ
ЃЌ![]() ЃЌМЦЫуЕУЕН
ЃЌМЦЫуЕУЕН![]() ЃЌ
ЃЌ![]() ЃЌдйИљОнЕШВюЪ§СаЙЋЪНМЦЫуЕУЕНД№АИ.
ЃЌдйИљОнЕШВюЪ§СаЙЋЪНМЦЫуЕУЕНД№АИ.
ЃЈ1ЃЉгЩЦЕТЪЗжВМжБЗНЭМПЩЕУ2018Фъет50ЛЇМвЭЅШЫОљФъДПЪеШыЕФЦНОљжЕЮЊ
![]()
![]() ЃЈдЊЃЉ.
ЃЈдЊЃЉ.
ЃЈ2ЃЉвРЬтвтЃЌПЩЕУЃК![]() ЃЌЙЪ
ЃЌЙЪ![]() ЃЌ
ЃЌ
Ыљвд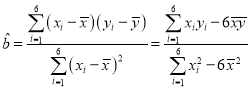
![]()
![]() .
.![]() ЃЌ
ЃЌ
Ыљвд![]() Йигк
Йигк![]() ЕФЯпадЛиЙщЗНГЬЮЊ
ЕФЯпадЛиЙщЗНГЬЮЊ![]() .
.
Сю![]() ЃЌЕУ2020Фъ1дТИУМвЭЅШЫОљдТДПЪеШыЮЊ
ЃЌЕУ2020Фъ1дТИУМвЭЅШЫОљдТДПЪеШыЮЊ![]() ЃЈдЊЃЉЃЌ
ЃЈдЊЃЉЃЌ
Сю![]() ЃЌЕУ2020Фъ12дТИУМвЭЅШЫОљдТДПЪеШыЮЊ
ЃЌЕУ2020Фъ12дТИУМвЭЅШЫОљдТДПЪеШыЮЊ![]() ЃЈдЊЃЉЃЌ
ЃЈдЊЃЉЃЌ
гЩЬтвтжЊЃЌИУМвЭЅЕФШЫОљдТДПЪеШыЕФЙРМЦжЕГЩЕШВюЪ§СаЃЌ
ЫљвдЃЌ2020ФъИУМвЭЅШЫОљФъДПЪеШыЕФЙРМЦжЕЮЊ![]() ЃЌ
ЃЌ
злЩЯЃЌдЄВтИУМвЭЅФмдк2020ФъЪЕЯжаЁПЕЩњЛю.

ЁОЬтФПЁПЯТБэЪЧФГЙЋЫО![]() Фъ
Фъ![]() дТЗнбаЗЂЗбгУ
дТЗнбаЗЂЗбгУ![]() ЃЈАйЭђдЊЃЉКЭВњЦЗЯњСП
ЃЈАйЭђдЊЃЉКЭВњЦЗЯњСП![]() ЃЈЭђЬЈЃЉЕФОпЬхЪ§ОнЃК
ЃЈЭђЬЈЃЉЕФОпЬхЪ§ОнЃК
дТ Зн |
|
|
|
|
|
|
|
|
баЗЂЗбгУЃЈАйЭђдЊЃЉ |
|
|
|
|
|
|
|
|
ВњЦЗЯњСПЃЈЭђЬЈЃЉ |
|
|
|
|
|
|
|
|
ЃЈ1ЃЉИљОнЪ§ОнПЩжЊ![]() гы
гы![]() жЎМфДцдкЯпадЯрЙиЙиЯЕЃЌгУЯпадЯрЙиЯЕЪ§ЫЕУї
жЎМфДцдкЯпадЯрЙиЙиЯЕЃЌгУЯпадЯрЙиЯЕЪ§ЫЕУї![]() гы
гы![]() жЎМфЕФЯрЙиадЧПШѕГЬЖШ
жЎМфЕФЯрЙиадЧПШѕГЬЖШ
ЃЈ2ЃЉЧѓГі![]() гы
гы![]() ЕФЯпадЛиЙщЗНГЬЃЈЯЕЪ§ОЋШЗЕН
ЕФЯпадЛиЙщЗНГЬЃЈЯЕЪ§ОЋШЗЕН![]() ЃЉЃЌВЂЙРМЦЕБбаЗЂЗбгУЮЊ
ЃЉЃЌВЂЙРМЦЕБбаЗЂЗбгУЮЊ![]() ЃЈАйЭђдЊЃЉЪБИУВњЦЗЕФЯњСП.
ЃЈАйЭђдЊЃЉЪБИУВњЦЗЕФЯњСП.
ВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
ВЮееЙЋЪНЃКЯрЙиЯЕЪ§ ЃЌЦфЛиЙщжБЯп
ЃЌЦфЛиЙщжБЯп![]() жаЕФ
жаЕФ