题目内容
(本小题满分14分)
已知椭圆 的左、右焦点分别为
的左、右焦点分别为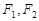 ,点
,点 是
是 轴上方椭圆
轴上方椭圆 上的一点,且
上的一点,且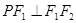 ,
, 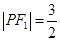 ,
,  .
.
(1)求椭圆 的方程和
的方程和 点的坐标;
点的坐标;
(2)判断以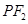 为直径的圆与以椭圆
为直径的圆与以椭圆 的长轴为直径的圆的位置关系.
的长轴为直径的圆的位置关系.
【答案】
(1)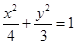 ,
, ;(2)两圆内切。
;(2)两圆内切。
【解析】
试题分析:(1) 在椭圆
在椭圆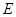 上
上  ,
……….2分
,
……….2分
 ,
,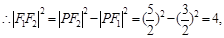 …….3分
…….3分
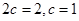 ,
, 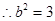 .
.
所以椭圆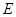 的方程是:
的方程是: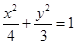 …………6分
…………6分
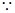
 ,
,

 …….8分
…….8分
(2)线段 的中点
的中点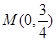
∴ 以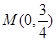 为圆心
为圆心 为直径的圆
为直径的圆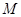 的方程为
的方程为
圆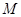 的半径
的半径 ………….10分
………….10分
以椭圆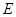 的长轴为直径的圆的方程为:
的长轴为直径的圆的方程为: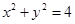 ,圆心为
,圆心为 ,半径为
,半径为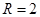
…11分
圆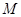 与圆
与圆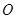 的圆心距为
的圆心距为 …….13分
…….13分
所以两圆内切.…….14分
考点:椭圆的定义;椭圆的标准方程;椭圆的简单性质;圆与圆的位置关系。
点评:圆与圆的位置关系:设两圆圆心分别为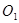 ,
, ,半径分别为
,半径分别为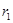 ,
, ,|
,|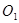
 |=d。 d>
|=d。 d>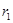 +
+ ?外离;d=
?外离;d=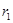 +
+ ?外切;|
?外切;|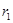 -
- |<d<
|<d<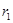 +
+ ?相交;d=|
?相交;d=|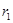 -
- |?内切;0<d<|
|?内切;0<d<|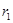 -
- |?内含.
|?内含.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)