题目内容

P的坐标（x，y）满足
x+y≤4
y≥x
x≥1
，过点P的直线l与圆C：x2+y2=14相交于A、B两点，则|AB|的最小值是（　　）
A、2
6
B、2
13
C、4
D、3
分析：满足条件的点P在直角三角形 MNR内，包括边界．此直角三角形中，只有点R（1，3），到圆心O 的距离最大，故当弦过点R且和OR垂直时，弦长最短．
解答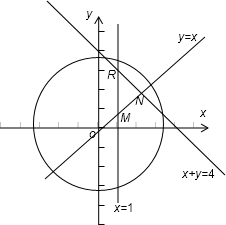：精英家教网解：如图：满足条件的点P在直角三角形 MNR内，包括边界．此直角三角形中，只有点R（1，3），
到圆心O 的距离最大，故当弦过点R且和OR垂直时，弦长最短．故最短弦长为
2
r2-OR2
=2
14 -10
=4，
故选 C．
点评：本题考查简单的线性规划问题，求两直线的交点坐标以及弦长公式的应用．
练习册系列答案
相关题目
以下五个关于圆锥曲线的命题中：
①平面内到定点A（1，0）和定直线l：x=2的距离之比为
1
2
的点的轨迹方程是
x2
4
+
y2
3
=1；
②点P是抛物线y2=2x上的动点，点P在y轴上的射影是M点A的坐标是A（3，6），则|PA|+|PM|的最小值是6；
③平面内到两定点距离之比等于常数λ（λ＞0）的点的轨迹是圆；
④若动点M（x，y）满足
(x-1)2+(y+2)2
=|2x-y-4|，则动点M的轨迹是双曲线；
⑤若过点C（1，1）的直线l交椭圆
x2
4
+
y2
3
=1于不同的两点A，B，且C是AB的中点，则直线l的方程是3x+4y-7=0．
其中真命题的序号是
 
．（写出所有真命题的序号）
点P（x，y）满足
x-y+1≥0
x+y≥0
x≤0
，点A的坐标是（1，2），若∠AOP=θ，则|
OP
|cosθ的最大值是
 
．
已知O为坐标原点，A（2，1），P（x，y）满足
x-4y+3≤0
3x+5y≤25
x-1≥0
，则|
OP
|•cos∠AOP的最大值等于
 
．
已知点P（x，y）满足
x-4y+3≤0
3x+5y≤25
x-1≥0
，设A（2，0），则|
OP
|sin∠AOP（O为坐标原点）的最大值为
22
5
22
5
．
（2009•孝感模拟）已知点P（x，y）满足
x-y+2≥0
2x+y-8≥0
x≤3
，则|
OP
|（O是坐标圆点）的最大值等于
34
34
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网