题目内容
已知点P（x，y）满足
，设A（2，0），则|
|sin∠AOP（O为坐标原点）的最大值为
．
|
| OP |
| 22 |
| 5 |
| 22 |
| 5 |
分析：画出不等式组的可行域，判断出目标函数的几何意义，结合图象得到最大值．
解答：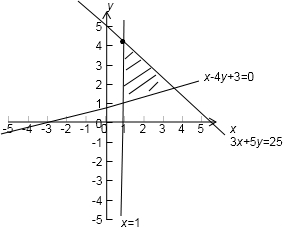
解：画出点P（x，y）满足
，可行域，
根据题意，
分析可得：
|
|sin∠AOP表示的是点P的纵坐标，
由图知，可行域中最上面的点（1，
）的纵坐标最大，
故答案为：
解：画出点P（x，y）满足
|
根据题意，
分析可得：
|
| OP |
由图知，可行域中最上面的点（1，
| 22 |
| 5 |
故答案为：
| 22 |
| 5 |
点评：本题主要考查了向量的数量积、简单的线性规划，以及利用几何意义求最值，巧妙识别目标函数的几何意义是我们研究规划问题的基础，纵观目标函数包括线性的与非线性，非线性问题的介入是线性规划问题的拓展与延伸，使得规划问题得以深化．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目