题目内容
(本题14分)如图:在二面角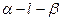 中,A、B
中,A、B ,C、D
,C、D ,ABCD为矩形,
,ABCD为矩形, 且PA=AD,M、N依次是AB、PC的中点,
且PA=AD,M、N依次是AB、PC的中点,

(1)求二面角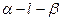 的大小(6分)
的大小(6分)
(2)求证: (6分)
(6分)
(1) 求异面直线PA和MN所成角的大小(7分)
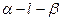 中,A、B
中,A、B ,C、D
,C、D ,ABCD为矩形,
,ABCD为矩形, 且PA=AD,M、N依次是AB、PC的中点,
且PA=AD,M、N依次是AB、PC的中点,
(1)求二面角
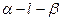 的大小(6分)
的大小(6分)(2)求证:
 (6分)
(6分)(1) 求异面直线PA和MN所成角的大小(7分)
(1)二面角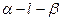 的平面角为450。(2)异面直线PA和MN所成的角为450
的平面角为450。(2)异面直线PA和MN所成的角为450
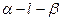 的平面角为450。(2)异面直线PA和MN所成的角为450
的平面角为450。(2)异面直线PA和MN所成的角为450
解:(1)连结PD∵ABCD为矩形∴AD⊥DC, 即
又PA⊥
 ,∴PD⊥
,∴PD⊥ ,
,∴
 PAD为二面角
PAD为二面角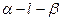 的平面角,又∵PA⊥AD,PA=AD
的平面角,又∵PA⊥AD,PA=AD∴
 PAD是等腰直角三角形,∴
PAD是等腰直角三角形,∴ PDA=450,即二面角
PDA=450,即二面角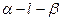 的平面角为450。
的平面角为450。(2)证明:过M作ME∥AD,交CD于E,连结NE,则ME⊥CD,
NE⊥CD,∴CD⊥平面MNE, MN⊥CD,又∵AB∥CD,MN⊥AB。
(3)解:过N作NF∥CD,交PD于F,∵ N是PC的中点
∴F是PD的中 点,连结AF,可以证明四边形AMNF是平行四边形
∴AF∥MN,
 PAF是异面直线PA和MN所成的角,∵ PA=PD, ∴F是PD的中点,∴AF是
PAF是异面直线PA和MN所成的角,∵ PA=PD, ∴F是PD的中点,∴AF是 PAD的平分线,∵
PAD的平分线,∵  PAD=900 ∴
PAD=900 ∴ PAF=450,∴异面直线PA和MN所成的角为450。
PAF=450,∴异面直线PA和MN所成的角为450。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
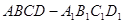 中,
中,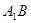 与
与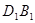 所成的角是( )
所成的角是( )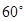 B.
B. 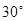 C.
C.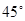 D.
D.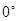
 中,
中, 分别是
分别是 和
和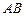 的中点,求异面直线
的中点,求异面直线 与
与 所成角的正切值
所成角的正切值
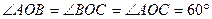 ,则交线OA与平面OBC所成的角的余弦值是( )
,则交线OA与平面OBC所成的角的余弦值是( ) B.
B. C.
C. D.
D.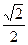

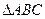 沿DE、EF、DF折成三棱锥P—DEF,如图所示,则异面直线PG与MN所成角的大小为 ▲
沿DE、EF、DF折成三棱锥P—DEF,如图所示,则异面直线PG与MN所成角的大小为 ▲ 




 ,B、C两点间的球面距离是
,B、C两点间的球面距离是 ,则二面角
,则二面角 的大小是
的大小是