题目内容

13．直线y=kx+1与圆x2+y2-2a2-2a-4=0恒有交点，则实数a的取值范围是a∈R．

分析 直线y=kx+1与曲线x2+y2-2a2-2a-4=0恒有交点，说明直线系过的定点必在圆上或圆内．

解答 解：直线y=kx+1恒过（0，1）点的直线系，
直线与曲线x2+y2-2a2-2a-4=0恒有交点，必须定点在圆上或圆内，
即：02+12-2a2-2a-4≤0，所以a∈R．
故答案为：a∈R．

点评 本题考查直线与圆的位置关系，点与圆的位置关系，两点间的距离公式，直线系等知识是中档题．

练习册系列答案
相关题目
3．已知函数y=f（x）x∈R 有下列4个命题：
①若f（1+x）=f（1-x），则f（x）的图象关于直线x=1对称；
②若f（3+x）+f（1-x）=4，则f（x）的图象关于点（2，2）对称；
③若f（x）为偶函数，且f（2+x）=-f（x），则f（x）的图象关于直线x=2对称；
④若f（x）为奇函数，且f（x）=f（-x-2），则f（x）的图象关于直线x=1对称．
其中正确的命题为①②③④．
4．函数y=x2-2x-3在x∈[-3，2]上的值域是[-4，12]．
1．设集台A={x|x＜5}，B={x|x≥-2}，则A∩B={x|-2≤x＜5}．
8．求下列函数的单调区间：
（1）y=-x2+2|x-1|+3；
（2）y=$\sqrt{{x}^{2}-6x+9}$+$\sqrt{{x}^{2}+6x+9}$．
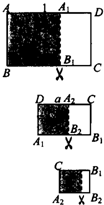18．长为1，宽为a（$\frac{1}{2}$＜a＜1）的矩形纸片，剪下一个边长等于矩形宽度的正方形（称为第1次操作），剩下矩形长为原矩形的宽，如图，再剪下一个边长等于此时矩形宽度的正方形（称为第2次操作），剩下矩形长为第二个矩形的宽，如此反复操作下去，若在第n次操作后，剩下的矩形为正方形，则操作终止．
（1）当a=$\frac{3}{5}$时，求正整数n的最大值；
（2）记第一个矩形的长为a1=1，第二个矩形的长为a2=a，以此类推，第n个矩形的长为an，数列{an}的前n项和为Sn．若存在一个正数a（$\frac{1}{2}$＜a＜1），使对于任意的正整数n（n≥3），都有an+1＜an，求证2＜Sn＜3．
5．已知f（n）=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$，且g（n）=$\frac{1}{f（n）-1}$[f（1）+f（2）+…十f（n-1）]．
（1）写出g（2），g（3），g（4）的值；
（2）归纳g（n）的值，并用数学归纳法加以证明．
2．（1）已知x，y∈R+，x≠y，求证：$\frac{1}{x}$$+\frac{1}{y}$$＞\frac{2}{x+y}$；
（2）如何改进上述结论，使之成为-个更好的结论．
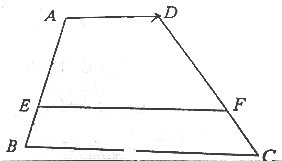3．如图，已知：梯形ABCD中，AD∥EF∥BC，AE=2BE，AD=2，BC=5，设$\overrightarrow{AD}$=$\overrightarrow{a}$，用$\overrightarrow{a}$表示$\overrightarrow{EF}$，$\overrightarrow{CB}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网