题目内容
【题目】已知数列![]() 、
、![]() 满足
满足![]() ,且
,且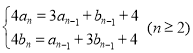
(1)令![]() 证明:
证明:![]() 是等差数列,
是等差数列,![]() 是等比数列;
是等比数列;
(2)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(3)求数列![]() 和
和![]() 的前n项和公式.
的前n项和公式.
【答案】(1)证明见解析;(2)![]() ,
,![]() ;(3)数列
;(3)数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() .
.
【解析】
(1)在等式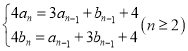 中将两式分别相加或相减,利用等差数列的定义可证明出数列
中将两式分别相加或相减,利用等差数列的定义可证明出数列![]() 是等差数列,利用等比数列的定义可证明出数列
是等差数列,利用等比数列的定义可证明出数列![]() 为等比数列;
为等比数列;
(2)求出数列![]() 、
、![]() 的通项公式,可建立关于
的通项公式,可建立关于![]() 、
、![]() 的方程组,解出
的方程组,解出![]() 、
、![]() ,即可得出数列
,即可得出数列![]() 和
和![]() 的通项公式;
的通项公式;
(3)利用分组求和法可求出数列![]() 和
和![]() 的前
的前![]() 项和.
项和.
(1)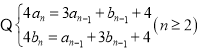 ,
,
将上述两等式相加得![]() ,
,
即![]() ,因此
,因此![]() ,又
,又![]() ,
,
所以数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,
的等差数列,![]() .
.
又由题设得![]() ,即
,即![]() ,
,
因此![]() ,又
,又![]() ,
,
所以数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,![]() ;
;
(2)由(1)知![]() ,
,![]() ,即
,即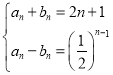 ,
,
解得![]() ,
,![]() ;
;
(3)设数列![]() 和
和![]() 的前
的前![]() 项和分别为
项和分别为![]() 、
、![]() ,
,
则![]()
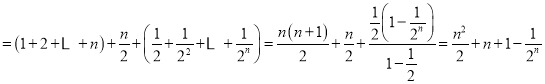 ,同理可得
,同理可得![]() .
.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目