题目内容
已知椭圆
+
=1的左、右焦点分别是F1、F2,P是椭圆上的一个动点,如果延长F1P到Q,使|PQ|=|PF2|,那么动点Q的轨迹方程为 .
| x2 |
| 9 |
| y2 |
| 4 |
考点:轨迹方程
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:由题意可知,点Q的轨迹是以F1(-
,0)为圆心,以|F1Q|=6为半径的圆,由此可求出其方程.
| 5 |
解答:
解:∵F1(-
,0),F2(
,0),|PF1|+|PF2|=2a=6,|PQ|=|F2P|,
∴|F1Q|=|F1P|+|F2P|=2a=6,
∴Q的轨迹是以F1(-
,0)为圆心,以|F1Q|=6为半径的圆,
其方程为(x+
)2+y2=36.
故答案为:(x+
)2+y2=36.
| 5 |
| 5 |
∴|F1Q|=|F1P|+|F2P|=2a=6,
∴Q的轨迹是以F1(-
| 5 |
其方程为(x+
| 5 |
故答案为:(x+
| 5 |
点评:本题考查椭圆的性质和圆的方程,解题要注意审题,避免出错.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
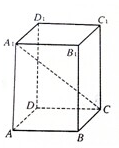 如图所示,四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,高A1A=3,体积为24,则对角线A1C为
如图所示,四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,高A1A=3,体积为24,则对角线A1C为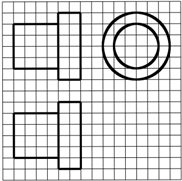 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6c m的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6c m的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为