题目内容
讨论下列椭圆的范围，并画出图形：
（1）4x2+y2=16；
（2）5x2+9y2=100．
（1）4x2+y2=16；
（2）5x2+9y2=100．
考点：椭圆的简单性质
专题：计算题,作图题,圆锥曲线的定义、性质与方程
分析：首先将椭圆方程化为标准方程，再由椭圆的几何性质，求得范围，并画出图形．
解答：
解：（1）4x2+y2=16即为
+
=1，
即有|x|≤4，|y|≤16，
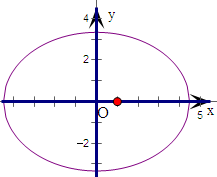
即有-4≤x≤4，-16≤y≤16，如右图；
（2）5x2+9y2=100即为
+
=1，
即有|x|≤2
，|y|≤
，
即有-2
≤x≤2
，-
≤y≤
如下图．
解：（1）4x2+y2=16即为| x2 |
| 4 |
| y2 |
| 16 |
即有|x|≤4，|y|≤16，
即有-4≤x≤4，-16≤y≤16，如右图；
（2）5x2+9y2=100即为
| x2 |
| 20 |
| y2 | ||
|
即有|x|≤2
| 5 |
| 10 |
| 3 |
即有-2
| 5 |
| 5 |
| 10 |
| 3 |
| 10 |
| 3 |
点评：本题考查椭圆的性质和图象，考查运算能力和作图能力，属于基础题．
练习册系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
定义在（-1，1）上的函数f（x）-f（y）=f（
）；当x∈（-1，0）时，f（x）＞0，若P=f（
）+f（
），Q=f（
），R=f（0），则P，Q，R的大小关系为（ ）
| x-y |
| 1-xy |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 3 |
| A、Q＞P＞R |
| B、P＞Q＞R |
| C、R＞Q＞P |
| D、R＞P＞Q |
如图，分别以正方形ABCD的四条边为直径画半圆，重叠部分如图中阴影区域．