题目内容
(本小题满分12分)已知数列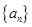 的前n项和
的前n项和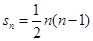 ,且
,且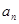 是
是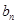 与1的等差中项。
与1的等差中项。
(1)求数列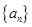 和数列
和数列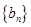 的通项公式;
的通项公式;
(2)若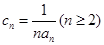 ,求
,求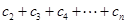
(3)若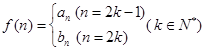 ,是否存在
,是否存在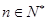 ,使得
,使得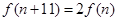 并说明理由。
并说明理由。
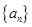 的前n项和
的前n项和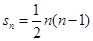 ,且
,且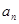 是
是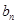 与1的等差中项。
与1的等差中项。(1)求数列
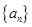 和数列
和数列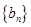 的通项公式;
的通项公式;(2)若
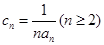 ,求
,求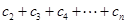
(3)若
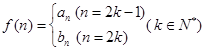 ,是否存在
,是否存在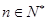 ,使得
,使得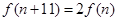 并说明理由。
并说明理由。(1)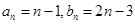 (2)
(2)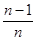 (3)当n为奇数时,
(3)当n为奇数时,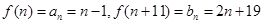 由已知得2n+19=2n-2,矛盾。当n为偶数时,
由已知得2n+19=2n-2,矛盾。当n为偶数时,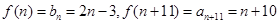 由已知得n+10=4n-6,矛盾。
由已知得n+10=4n-6,矛盾。
所以满足条件的n不存在。
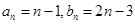 (2)
(2)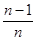 (3)当n为奇数时,
(3)当n为奇数时,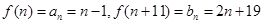 由已知得2n+19=2n-2,矛盾。当n为偶数时,
由已知得2n+19=2n-2,矛盾。当n为偶数时,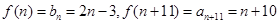 由已知得n+10=4n-6,矛盾。
由已知得n+10=4n-6,矛盾。所以满足条件的n不存在。
试题分析:(1)
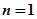 时,
时,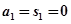 ,
,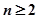 时,
时,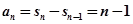 ,综上
,综上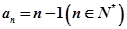 ,
,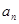 是
是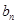 与1的等差中项
与1的等差中项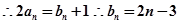
(2)
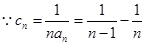

(3)
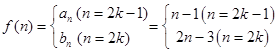
当n为奇数时,
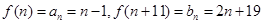 由已知得2n+19=2n-2,n无解
由已知得2n+19=2n-2,n无解当n为偶数时,
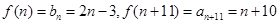 由已知得n+10=4n-6,
由已知得n+10=4n-6,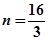
所以满足条件的n不存在
点评:由数列的
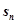 求通项
求通项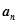 时需分
时需分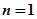 与
与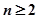 两种情况讨论,
两种情况讨论,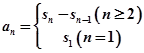 ,第二问一般数列求和采用的是裂项相消的方法,适用于通项为
,第二问一般数列求和采用的是裂项相消的方法,适用于通项为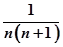 形式的数列
形式的数列
练习册系列答案
相关题目
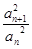 =p(p为正常数,n∈N+),则称{an}为“等方比数列”.
=p(p为正常数,n∈N+),则称{an}为“等方比数列”.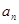 }的前
}的前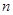 项和
项和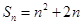 ,
,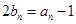 ,且
,且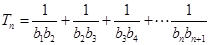 ,求
,求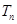 .
.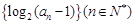 为等差数列,且
为等差数列,且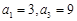
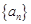 的通项公式;
的通项公式;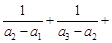 …
…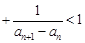 .
.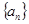 为单调递增的等差数列,
为单调递增的等差数列,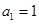 ,且
,且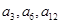 依次成等比数列.
依次成等比数列.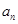 ;
; ,求数列
,求数列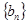 的前
的前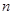 项和
项和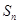 ;
;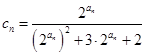 ,求数列
,求数列 的前
的前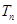 .
.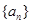 前
前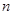 项和
项和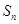 满足
满足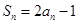 ,等差数列
,等差数列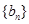 满足
满足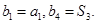
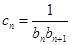 ,数列
,数列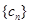 的前
的前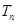 ,问
,问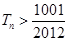 的最小正整数n是多少?
的最小正整数n是多少?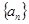 是递增数列,且满足
是递增数列,且满足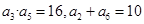 。
。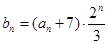 ,求数列
,求数列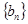 的前
的前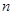 项和
项和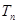 。
。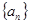 的前
的前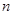 项和为
项和为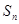 ,已知
,已知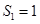 ,
,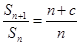 (
(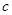 为常数,
为常数,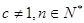 ),且
),且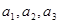 成等差数列.
成等差数列.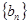 是首项为1,公比为
是首项为1,公比为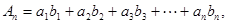
 ,(
,(