Question

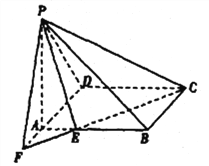
【题目】如图，在四棱锥P﹣ABCD中，PA⊥底面ABCD，BC⊥PB，△BCD为等边三角形，PA=BD= ，AB=AD，E为PC的中点．

（1）求证：BC⊥AB；
（2）求AB的长；
（3）求平面BDE与平面ABP所成二面角的正弦值．

Answer 1

【答案】
（1）证明：连结AC，

∵PA⊥底面ABCD，BC平面ABCD，∴PA⊥BC，

又∵BC⊥PB，PA∩PB=P，∴BC⊥平面PAB，

∵AB平面PAB，

∴AB⊥BC

（2）解：由（1）知AB⊥BC，

∵△BCD为等边三角形，∴∠ABD=30°，

又AB=AD， ，

解得AB=1

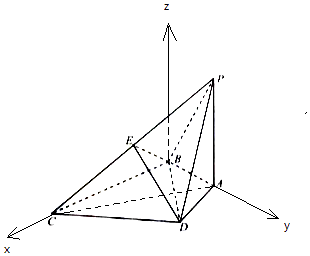
（3）解：分别以BC，BA所在直线为x，y轴，过B且平行PA的直线为z轴，建立空间直角坐标系，

， ， ， ．

由题意可知平面PAB的法向量 ，

设平面BDE的法向量为 ，

则 即 ，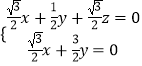

取x=3，得 ，

，

∴平面BDE与平面ABP所成二面角的正弦值为 ．

【解析】（1）连结AC，推导出PA⊥BC，BC⊥PB，从而BC⊥平面PAB，由此能证明AB⊥BC．（2）推导出AB⊥BC，∠ABD=30°，由此能求出AB．（3）分别以BC，BA所在直线为x，y轴，过B且平行PA的直线为z轴，建立空间直角坐标系，利用向量法能求出平面BDE与平面ABP所成二面角的正弦值．
【考点精析】解答此题的关键在于理解直线与平面垂直的性质的相关知识，掌握垂直于同一个平面的两条直线平行．