题目内容
【题目】已知p：实数x满足x2﹣4ax+3a2＜0，其中a＞0； q：实数x满足2＜x≤3．
（1）若a=1，且p∧q为真，求实数x的取值范围；
（2）若p是q的必要不充分条件，求实数a的取值范围．
【答案】
（1）解：p：由原不等式得，（x﹣3a）（x﹣a）＜0，∵a＞0为，所以a＜x＜3a；
当a=1时，得到1＜x＜3；
q：实数x满足2＜x≤3；
若p∧q为真，则p真且q真，∴实数x的取值范围是：（2，3）
（2）解：p是q的必要不充分条件，即由p得不到q，而由q能得到p；
∴ 
，解得1≤a≤2；
∴实数a的取值范围是[1，2]
【解析】（1）先通过解一元二次不等式求出p下的x的取值范围：a＜x＜3a，a=1时，所以p：1＜x＜3．根据p∧q为真得p，q都真，所以 
，所以解该不等式组即得x的取值范围；（2）若p是q的必要不充分条件，则： ，所以解该不等式组即得a的取值范围．
【考点精析】掌握复合命题的真假是解答本题的根本，需要知道“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反；“p且q”形式复合命题当P与q同为真时为真，其他情况时为假；“p或q”形式复合命题当p与q同为假时为假，其他情况时为真．
【题目】某校高一年级共有1000名学生，其中男生400名，女生600名，该校组织了一次口语模拟考试（满分为100分）．为研究这次口语考试成绩为高分（80分以上（含80分）为高分）是否与性别有关，现按性别采用分层抽样的方法抽取100名学生的成绩，按从低到高分成
七组，并绘制成如图所示的频率分布直方图．已知区间
上的频率等于区间
上频率，区间
上的频率与区间
上的频率之比为
．
| 0．010 | 0．050 | 0．025 | 0．010 | 0．001 |
| 6．635 | 3．841 | 5．024 | 6．635 | 10．828 |
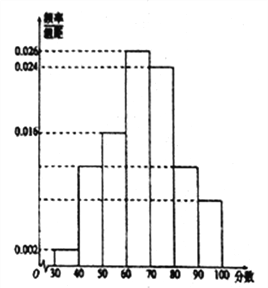
（1）估计该校高一年级学生在口语考试中，成绩为高分的人数；
（2）请你根据已知条件将下列
列联表补充完整，并判断是否有
的把握认为“该校高一年级学生在本次考试中口语成绩及格（60分以上（含60分）为及格）与性别有关”．
附： 
