题目内容
已知在等比数列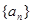 中,
中,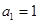 ,且
,且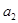 是
是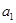 和
和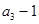 的等差中项.
的等差中项.
(Ⅰ)求数列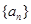 的通项公式;
的通项公式;
(Ⅱ)若数列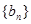 满足
满足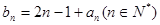 ,求
,求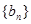 的前
的前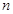 项和
项和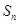 .
.
(Ⅰ)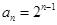 ;(Ⅱ)
;(Ⅱ)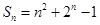 .
.
解析试题分析:(Ⅰ)设公比是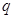 ,依据等比数列的通项公式表示出
,依据等比数列的通项公式表示出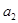 和
和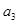 ,再由已知条件“
,再由已知条件“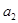 是
是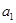 和
和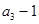 的等差中项”,结合等差中项的性质得到
的等差中项”,结合等差中项的性质得到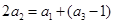 ,解出
,解出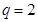 ,代入等比数列的通项公式;(Ⅱ)先由(Ⅰ)中解得的
,代入等比数列的通项公式;(Ⅱ)先由(Ⅰ)中解得的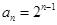 ,求出数列
,求出数列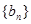 的通项公式:
的通项公式: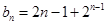 ,观察可知它可以分为一个等差数列
,观察可知它可以分为一个等差数列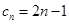 和一个等比数列
和一个等比数列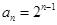 ,结合等差数列和等比数列的前
,结合等差数列和等比数列的前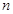 项和公式求
项和公式求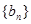 的前
的前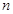 项和
项和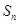 .
.
试题解析:(Ⅰ)设公比为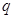 ,
,
则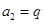 ,
,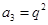 ,
,
∵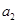 是
是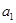 和
和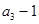 的等差中项,
的等差中项,
∴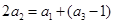 ,
,
即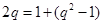
解得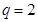 ,
,
∴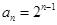 .
.
(Ⅱ)由(Ⅰ)可知,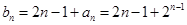 ,
,
则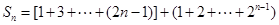
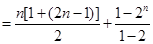
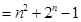 .
.
考点:1.等差数列的前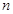 项和;2.等比数列的前
项和;2.等比数列的前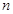 项和;3.等差中项;4.等比数列的通项公式
项和;3.等差中项;4.等比数列的通项公式

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
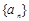 满足
满足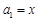 ,
,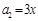 ,
,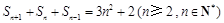 ,
,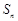 是数列
是数列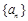 的前
的前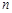 项和.
项和.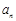 ;
;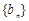 满足
满足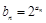 ,数列
,数列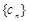 满足
满足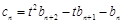 ,试比较数列
,试比较数列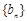 前
前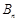 与
与 的大小;
的大小;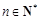 ,
,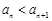 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.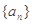 中,公差
中,公差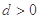 ,其前
,其前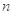 项和为
项和为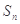 ,且满足:
,且满足: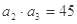 ,
,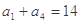 .
.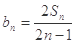 ,
,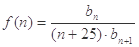 (
(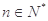 ),求
),求 的最大值.
的最大值.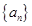 的前
的前 项和为
项和为 ,且满足
,且满足 ,其中
,其中 、
、 、
、 是常数.
是常数. ,
, ,
, ,求数列
,求数列 ,
, ,
, ,且
,且 ,求数列
,求数列 的等比数列.
的等比数列.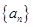 的前
的前 项和为
项和为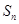 ,且
,且
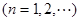 .
.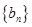 满足
满足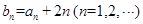 ,求数列
,求数列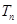 .
.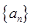 满足:
满足: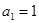 ,
,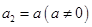 ,
,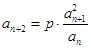 (其中
(其中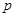 为非零常数,
为非零常数,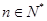 ).
).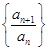 是不是等比数列?
是不是等比数列?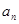 ;
;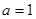 时,令
时,令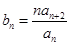 ,
,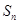 为数列
为数列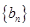 的前
的前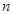 项和,求
项和,求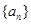 的首项
的首项 ,且满足
,且满足
 ,求证:数列
,求证:数列 是等差数列,并求数列
是等差数列,并求数列 ,求数列
,求数列 的前n项和
的前n项和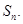
 的前n项和为
的前n项和为 ,已知
,已知 ,
, ,数列
,数列 是公差为d的等差数列,
是公差为d的等差数列, .
. .
.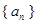 是首项为
是首项为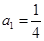 ,公比
,公比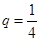 的等比数列.设
的等比数列.设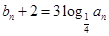 ,
,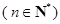 ,数列
,数列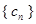 满足
满足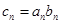 ;
;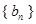 成等差数列;
成等差数列; 项和
项和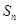 ;
;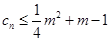 对一切正整数
对一切正整数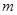 的取值范围.
的取值范围.