题目内容
设数列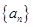 的前
的前 项和为
项和为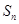 ,且
,且
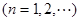 .
.
(1)证明:数列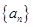 是等比数列;
是等比数列;
(2)若数列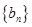 满足
满足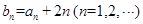 ,求数列
,求数列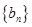 的前
的前 项和为
项和为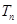 .
.
(1)参考解析;(2)
解析试题分析:(1)依题意可得递推一个等式然后对减即可得到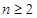 的通项公式.再检验n=1时的情况即可.
的通项公式.再检验n=1时的情况即可.
(2)由(1)可得等比数列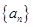 的通项公式.从而得到
的通项公式.从而得到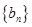 的通项公式
的通项公式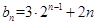 .求数列
.求数列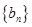 的前n项和在该通项公式中是一个等比数列和一个等差数列相加.所以是分别对两个数列求和再相加即可.本题(1)是数列中常见的知识点,通过递推在求差把含和的等式转化为只有通项的形式.对于(2)的通项公式是一个和的形式.所以利用两种形式要分开求.
的前n项和在该通项公式中是一个等比数列和一个等差数列相加.所以是分别对两个数列求和再相加即可.本题(1)是数列中常见的知识点,通过递推在求差把含和的等式转化为只有通项的形式.对于(2)的通项公式是一个和的形式.所以利用两种形式要分开求.
试题解析:(1)证明:因为
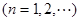 ,
,
则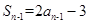
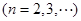 1分
1分
所以当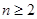 时,
时,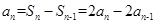 ,
,
整理得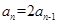 .由
.由 ,令
,令 ,得
,得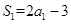 ,解得
,解得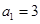 .
.
所以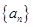 是首项为3,公比为2的等比数列. 6分
是首项为3,公比为2的等比数列. 6分
(2)解:因为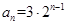 ,由
,由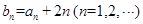 ,得
,得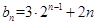 .
.
所以

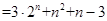
所以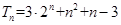 . 12分
. 12分
考点:1.数列的递推形式.2.等比数列求和.3.等差数列求和.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
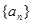 是公差不为零的等差数列,
是公差不为零的等差数列,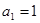 ,且
,且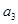 是
是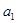 和
和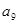 的等比中项.
的等比中项.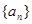 的通项公式;
的通项公式;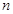 项和为
项和为 ,
,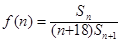 ,试问当
,试问当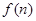 最大?并求出
最大?并求出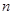 个月月底余
个月月底余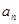 元,第
元,第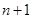 个月月底余
个月月底余 元,写出
元,写出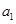 的值并建立
的值并建立 中,
中, ,
, ,
, .
. 是等比数列,并求数列
是等比数列,并求数列 且
且 ,
, ,求证:使得
,求证:使得 ,
, ,
, 成等差数列的点列
成等差数列的点列 在某一直线上.
在某一直线上. 中,公差
中,公差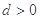 ,其前
,其前 项和为
项和为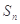 ,且满足:
,且满足: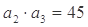 ,
, .
. ,
, ,求
,求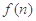 的最小值.
的最小值.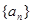 中,
中,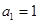 ,且
,且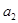 是
是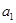 和
和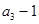 的等差中项.
的等差中项.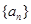 的通项公式;
的通项公式;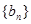 满足
满足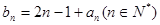 ,求
,求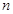 项和
项和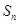 .
.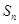 为数列
为数列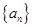 的前
的前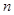 项和,且有
项和,且有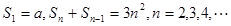
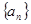 是单调递增数列,求
是单调递增数列,求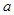 的取值范围.
的取值范围.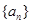 满足:
满足: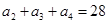 ,且
,且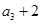 是
是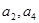 的等差中项.
的等差中项.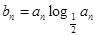 ,
,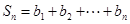 ,求使
,求使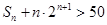 成立的正整数
成立的正整数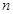 的最小值.
的最小值.