题目内容
已知数列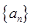 满足:
满足: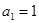 ,
,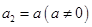 ,
,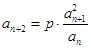 (其中
(其中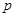 为非零常数,
为非零常数,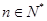 ).
).
(1)判断数列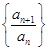 是不是等比数列?
是不是等比数列?
(2)求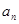 ;
;
(3)当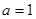 时,令
时,令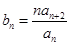 ,
,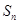 为数列
为数列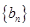 的前
的前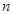 项和,求
项和,求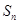 .
.
(1)数列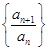 是等比数列;(2)
是等比数列;(2)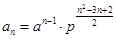 ,
,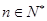 ;(3)
;(3)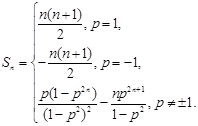 .
.
解析试题分析:(1)将数列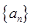 的递推式
的递推式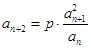 进行变形得
进行变形得 ,从而利用定义得到数列
,从而利用定义得到数列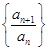 是等比数列;(2)在(1)的基础上先求出数列
是等比数列;(2)在(1)的基础上先求出数列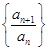 的通项公式,再利用累乘法求数列
的通项公式,再利用累乘法求数列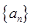 的通项公式;(3)在(2)的基础上,将
的通项公式;(3)在(2)的基础上,将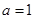 代入数列
代入数列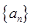 的通项公式,从而求出数列
的通项公式,从而求出数列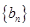 的通项公式,并根据数列
的通项公式,并根据数列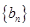 的通项公式
的通项公式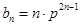 ,对
,对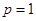 、
、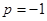 以及
以及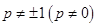 进行三种情况的分类讨论,前两种情况利用等差数列求和即可,在最后一种情况下利用错位相减法求数列
进行三种情况的分类讨论,前两种情况利用等差数列求和即可,在最后一种情况下利用错位相减法求数列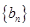 的前
的前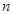 项和
项和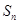 ,最后用分段的形式表示数列
,最后用分段的形式表示数列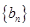 的前
的前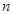 项和
项和 .
.
试题解析:(1)由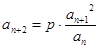 ,得
,得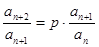 .
.
令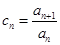 ,则
,则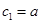 ,
,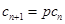 .
.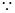
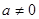 ,
, ,
,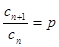 (非零常数),
(非零常数),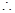 数列
数列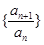 是等比数列.
是等比数列.
(2)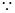 数列
数列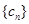 是首项为
是首项为 ,公比为
,公比为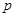 的等比数列,
的等比数列,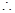
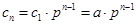 ,即
,即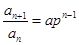 .
.
当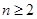 时,
时,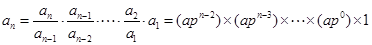
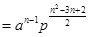 ,
,
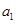 满足上式,
满足上式,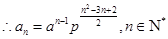 .
.
(3)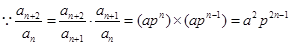 ,
,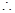 当
当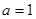 时,
时,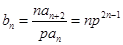 .
.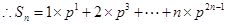 , ①
, ①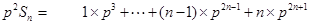 ②
②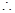 当
当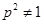 ,即
,即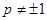 时,①
时,① ②得:
②得: ,
,
即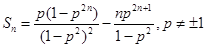 .
.
而当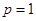 时,
时,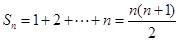 ,
,
当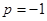 时,
时,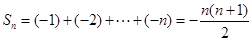 .
.
综上所述,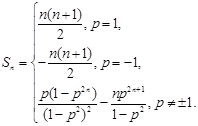
考点:1.定义法证明等比数列;2.累乘法求数列通项;3.等差数列求和;4.错位相减法求和

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
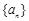 的前
的前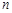 项和为
项和为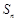 ,已知
,已知 ,
,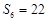 .
.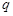 的等比数列
的等比数列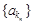 ,其中
,其中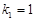 ,且
,且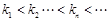 ,
,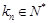 .
.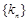 的通项公式;
的通项公式; 的不等式
的不等式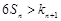 有解,试求
有解,试求 前n项和为
前n项和为 ,首项为
,首项为 ,且
,且 成等差数列.
成等差数列.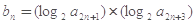 ,求证:
,求证: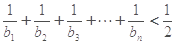
 是等差数列
是等差数列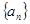 的前
的前 项和,满足
项和,满足 ;
;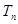 是数列
是数列 的前
的前 .
. 的前
的前 .
.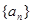 中,
中,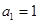 ,且
,且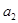 是
是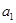 和
和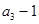 的等差中项.
的等差中项.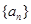 的通项公式;
的通项公式;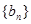 满足
满足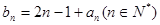 ,求
,求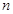 项和
项和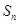 .
. 为等比数列,
为等比数列,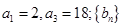 是等差数列,
是等差数列,
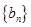 的通项公式及前
的通项公式及前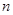 项和
项和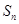 ;
;
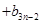 ,
,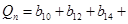
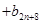 ,其中
,其中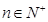 ,试比较
,试比较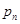 与
与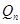 的大小,并加以证明.
的大小,并加以证明.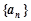 的前
的前 项和
项和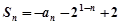 ,
, .
. 是等差数列;
是等差数列; ,求数列
,求数列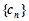 的前
的前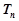 .
. 是等差数列,
是等差数列, 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且 ,
,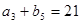 ,
,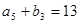 .
. 的前
的前 项和
项和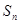 .
.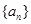 为等差数列,数列
为等差数列,数列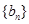 为等比数列且公比大于1,若
为等比数列且公比大于1,若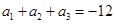 ,
,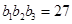 ,且
,且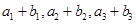 恰好是一各项均为正整数的等比数列的前三项.
恰好是一各项均为正整数的等比数列的前三项.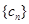 满足
满足
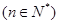 ,求
,求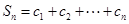 .
.