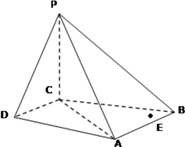Question

【题目】如图，在 中， ， ，点 在 边上，且 ， ．

（I）求 ；
（II）求 的长．

Answer 1

【答案】解：（I）在 中，∵ ，∴

∴

（II）在 中，由正弦定理得：

在 中，由余弦定理得：

∴

【解析】（I）根据同角三角函数基本关系式sin2+co2=1可求出sin，再根据三角形的一个外角等于与它不相邻的两个内角和，将用和表示，然后利用两角差的正弦公式即可求解；（II）在中，由正弦定理可得：=，而=，从而可求出BD的长；在中，由余弦定理可知：AC2=AB2+BC2-2ABBCcosB，进而可求出AC的长.
【考点精析】解答此题的关键在于理解两角和与差的正弦公式的相关知识，掌握两角和与差的正弦公式：，以及对正弦定理的定义的理解，了解正弦定理:．