Question

【题目】已知长方体ABCD﹣A1B1C1D1中，底面ABCD为正方形，DD1⊥平面ABCD，AB=4，AA1=2，点E1在棱C1D1上，且D1E1=3．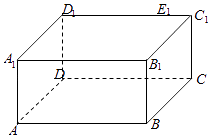

（Ⅰ）在棱CD上确定一点E，使得直线EE1∥平面D1DB，并写出证明过程；
（Ⅱ）若动点F在正方形ABCD内，且AF=2，请说明点F的轨迹，探求E1F长度的最小值并求此时直线E1F与平面ABCD所成角的正弦值．

Answer 1

【答案】解：（Ⅰ）连接D1B，DB，当DE=3时，直线EE1∥平面D1DB，

证明：∵DE∥D1E1，DE=D1E1，∴四边形DEE1D1为平行四边形，

∵EE1∥DD1，DD1平面D1DB，EE1平面D1DB，

∴直线EE1∥平面D1DB；

（Ⅱ）∵动点F在正方形ABCD内，且AF=2，∴点F的轨迹为以A为圆心，以2为半径的 圆周．

连接AE，则AE= =5，∴EF的最短距离为AE﹣AF=3，

∵E1F= ，∴E1F的长度最小值为 = ．

∵EE1⊥平面ABCD，∴∠E1FE为线E1F与平面ABCD所成的角

∴sin∠E1FE= = = ，即直线E1F与平面ABCD所成的角的正弦值为 ．

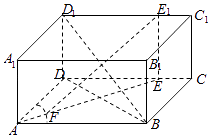
【解析】（Ⅰ）由题意可知连接D1B，DB，当DE=3时，根据线面平行的判定定理可证直线EE1∥平面D1DB。
（Ⅱ）由题意可得动点F在正方形ABCD内，且AF=2，∴点F的轨迹为以A为圆心，以2为半径的 圆，连接AE，EF的最短距离为AE﹣AF=3，根据勾股定理可得E1F的长度最小值为.再由线面角的定义找出∠E1FE为线E1F与平面ABCD所成的角，由可求得正弦值.
【考点精析】认真审题，首先需要了解棱柱的结构特征(两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形)．