题目内容
15.已知f(x)=$\frac{1+2lnx}{{x}^{2}}$.(1)求f(x)的单调区间;
(2)令g(x)=ax2-2lnx,则g(x)=1时有两个不同的根,求a的取值范围;
(3)存在x1,x2∈(1,+∞)且x1≠x2,使|f(x1)-f(x2)|≥k|lnx1-lnx2|成立,求k的取值范围.
分析 (1)求导f′(x)=-$\frac{4xlnx}{{x}^{4}}$=-$\frac{4lnx}{{x}^{3}}$,从而讨论导数的正负,以确定函数的单调性;
(2)化简可得a=$\frac{1+2lnx}{{x}^{2}}$=f(x),从而由(1)作函数的图象,从而解得;
(3)不妨设x1>x2>1,从而化不等式为函数h(x)=f(x)+klnx在(1,+∞)上存在单调减区间,从而可得h′(x)=f′(x)+$\frac{k}{x}$=-$\frac{4lnx}{{x}^{3}}$+$\frac{k}{x}$=$\frac{k{x}^{2}-4lnx}{{x}^{3}}$<0在(1,+∞)上有解,从而解得.
解答 解:(1)∵f(x)=$\frac{1+2lnx}{{x}^{2}}$,
f′(x)=$\frac{\frac{2}{x}•{x}^{2}-(1+2lnx)•2x}{{x}^{4}}$=-$\frac{4xlnx}{{x}^{4}}$=-$\frac{4lnx}{{x}^{3}}$,
故x∈(0,1)时,f′(x)>0,
x∈(1,+∞)时,f′(x)<0,
故f(x)在(0,1)上单调递增,在(1,+∞)上单调递减;
(2)∵g(x)=ax2-2lnx=1,
∴a=$\frac{1+2lnx}{{x}^{2}}$=f(x),
作函数f(x)的图象如下,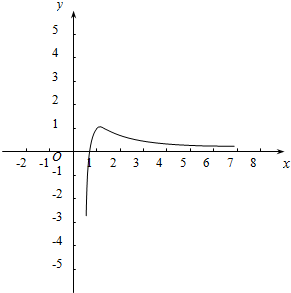 ,
,
∵f(1)=$\frac{1}{1}$=1,
∴结合图象可知,a的取值范围为(0,1);
(3)不妨设x1>x2>1,
∵f(x)在(1,+∞)上单调递减,y=lnx在(1,+∞)上单调递增;
∴|f(x1)-f(x2)|≥k|lnx1-lnx2|可化为
f(x2)-f(x1)≥k(lnx1-lnx2),
∴f(x2)+klnx2≥f(x1)+klnx1,
即函数h(x)=f(x)+klnx在(1,+∞)上存在单调减区间,
即h′(x)=f′(x)+$\frac{k}{x}$=-$\frac{4lnx}{{x}^{3}}$+$\frac{k}{x}$=$\frac{k{x}^{2}-4lnx}{{x}^{3}}$<0在(1,+∞)上有解,
即m(x)=kx2-4lnx<0在(1,+∞)上有解,
即k<$\frac{4lnx}{{x}^{2}}$在(1,+∞)上有解,
∵($\frac{4lnx}{{x}^{2}}$)′=$\frac{4-8lnx}{{x}^{3}}$,当x=$\sqrt{e}$时,$\frac{4-8lnx}{{x}^{3}}$=0;
故($\frac{4lnx}{{x}^{2}}$)max=$\frac{2}{e}$;
∴k<$\frac{2}{e}$.
点评 本题考查了导数综合应用及数形结合的思想应用,同时考查了学生由繁化简的能力.

| A. | {-4,-3,0,2,3} | B. | {-3,-2,0,1,3} | C. | {-3,-1,0,1,2} | D. | {-4,-3,0,1,2} |
| A. | 1 | B. | i | C. | -1 | D. | -i |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 相交 | B. | 异面 | C. | 平行 | D. | 相交或异面 |
| A | B | C | D | |
| 平均亩产量$\overline x$(kg) | 830 | 890 | 890 | 870 |
| 方差s2 | 3.5 | 3.7 | 2.5 | 6.0 |
| A. | A种子 | B. | B种子 | C. | C种子 | D. | D种子 |
| A. | 1-2a2 | B. | 1+2a2 | C. | 1-a2 | D. | a2-1 |