题目内容

6．函数f（x）=$\frac{1}{ln（x+1）}$的定义域为（-1，0）∪（0，+∞）．

分析 由分式的分母不为0，对数式的真数大于0联立不等式组得答案．

解答 解：要使原函数有意义，则$\left\{\begin{array}{l}{x+1＞0}\\{x+1≠1}\end{array}\right.$，
解得：x＞-1且x≠0．
∴函数$f（x）=\frac{1}{ln（x+1）}$的定义域为（-1，0）∪（0，+∞）．
故答案为：（-1，0）∪（0，+∞）．

点评 本题考查函数的定义域及其求法，是基础的计算题．

练习册系列答案
相关题目
16．如图是偶函数y=f（x）的局部图象，根据图象所给信息，下列结论正确的是（　　）
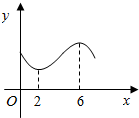
A．f（-2）-f（6）=0B．f（-2）-f（6）＜0C．f（-2）+f（6）=0D．f（-2）-f（6）＞0
17．设定义域为R的函数f（x）=$\left\{\begin{array}{l}{\frac{1}{|x-1|}（x≠1）}\\{1（x=1）}\end{array}\right.$，若关于x的方程f2（x）+bf（x）+c=0有5个不同的实数解，则b+c值为（　　）
A．0B．1C．-1D．不能确定
14．若函数f（x）=x3-px2-qx的图象与x轴相切于点（1，0），则f（x）的单调增区间为（-∞，$\frac{1}{3}$）或（1，+∞）．
1．对于任意的$m∈[\frac{1}{2}，3]$，不等式t2+mt＞2m+4恒成立，则实数t的取值范围是（-∞，-5）∪（2，+∞）．
11．已知定义在（0，+∞）上的函数f（x）为单调函数，且$f（{f（x）-\frac{4}{x}}）=4$，则f（1）=6．
18．已知函数$f（x）=\frac{{{2^x}-1}}{{{2^x}+1}}$的定义域为[-3，3]．
（1）判断函数f（x）的单调性，并用定义给出证明；
（2）若实数m满足f（m-1）＜f（1-2m），求m的取值范围．
15．已知f（x）=$\frac{1+2lnx}{{x}^{2}}$．
（1）求f（x）的单调区间；
（2）令g（x）=ax2-2lnx，则g（x）=1时有两个不同的根，求a的取值范围；
（3）存在x1，x2∈（1，+∞）且x1≠x2，使|f（x1）-f（x2）|≥k|lnx1-lnx2|成立，求k的取值范围．
16．已知数列{an}为等比数列，其前n项和为Sn，且S1，S2的等差中项为S3，若8（a1+a3）=-5．
（1）求数列[an]的通项公式；
（2）记Rn=|$\frac{1}{a_1}|+|\frac{2}{a_2}|+|\frac{3}{a_3}|+…+|\frac{n}{a_n}$|，对于任意的n≥2，n∈N*，不等式m（Rn-n-1）≥（n-1）2恒成立，求实数m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网