题目内容
5.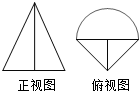 由两个简单几何体构成的组合几何体的三视图中,正视图和俯视图如右图所示,其中正视图中等腰三角形的高为3,俯视图中的三角形均为等腰直角三角形,半圆直径为2,则该几何体的体积为( )
由两个简单几何体构成的组合几何体的三视图中,正视图和俯视图如右图所示,其中正视图中等腰三角形的高为3,俯视图中的三角形均为等腰直角三角形,半圆直径为2,则该几何体的体积为( )| A. | $\frac{π}{2}+1$ | B. | π+1 | C. | $\frac{π}{2}+3$ | D. | π+3 |
分析 由已知中的三视力可得该几何体是一个半圆锥和三棱锥的组合体,计算出底面面积和高,代入锥体体积公式,可得答案.
解答 解:由已知中的三视力可得该几何体是一个半圆锥和三棱锥的组合体,
其底面面积S=$\frac{1}{2}$π+$\frac{1}{2}×2×1$=$\frac{1}{2}$π+1,
高h=3,
故该几何体的体积S=$\frac{1}{3}$Sh=$\frac{1}{2}$π+1,
故选:A
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
7.已知$\overrightarrow{a}$=($\sqrt{3}$,1),$\overrightarrow{b}$=(-3,$\sqrt{3}$),则<$\overrightarrow{a}$,$\overrightarrow{b}$>=( )
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
16.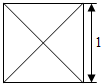 已知某几何体的俯视图是如图所示的边长为1的正方形,主视图与左视图是边长为1的正三角形,则其全面积是( )
已知某几何体的俯视图是如图所示的边长为1的正方形,主视图与左视图是边长为1的正三角形,则其全面积是( )
 已知某几何体的俯视图是如图所示的边长为1的正方形,主视图与左视图是边长为1的正三角形,则其全面积是( )
已知某几何体的俯视图是如图所示的边长为1的正方形,主视图与左视图是边长为1的正三角形,则其全面积是( )| A. | 2 | B. | 3 | C. | $1+\sqrt{3}$ | D. | $\sqrt{3}$ |
13.如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
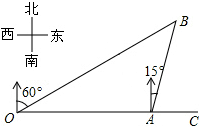

| A. | 4km | B. | 2$\sqrt{3}$km | C. | 2$\sqrt{2}$km | D. | ($\sqrt{3}$+1)km |
20.某几何体的三视图如图所示,则该几何体的体积是( )


| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{3}$ |
17. 用大小和形状完全相同的小正方体木块搭成一个几何体,使得它的主视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为( )
用大小和形状完全相同的小正方体木块搭成一个几何体,使得它的主视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为( )
 用大小和形状完全相同的小正方体木块搭成一个几何体,使得它的主视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为( )
用大小和形状完全相同的小正方体木块搭成一个几何体,使得它的主视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为( )| A. | 22个 | B. | 19个 | C. | 16个 | D. | 13个 |
14.双曲线x2-y2=1右支上一点P(a,b)到直线l:y=x的距离d=$\sqrt{2}$.则a+b=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{2}$或-$\frac{1}{2}$ | D. | 2或-2 |