题目内容
(12分)一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1、2、3、4,现从盒子中随机抽取卡片.
(Ⅰ)若一次从中随机抽取3张卡片,求3张卡片上数字之和大于或等于7的概率;
(Ⅱ)若第一次随机抽取1张卡片,放回后再随机抽取1张卡片,求两次抽取的卡片中至少一次抽到数字2的概率.
(Ⅰ) (Ⅱ)
(Ⅱ)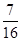
解析试题分析:(Ⅰ)写出任取三张的所有可能的结果,然后找出数字之和大于或等于2的结果,最后根据随机事件的概率公式求解即可.(Ⅱ)写出每次抽1张,连续抽取两张所有可能的结果,然后找出含有数字2的所有结果,最后根据随机事件的概率公式求解即可.
试题解析:(1)设A表示事件“抽取3张卡片上的数字之和大于或等于7”,
任取三张卡片,三张卡片上的数字全部可能的结果是(1、2、3),(1、2、4),(1、3、4),(2、3、4),共4种 2分
其中数字之和大于或等于7的是(1、2、4),(1、3、4),(2、3、4),
共3种 4分
所以P(A)= . 6分
. 6分
(2)设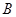 表示事件“至少一次抽到2”,
表示事件“至少一次抽到2”,
每次抽1张,连续抽取两张全部可能的结果有:(1、1)(1、2)(1、3)(1、4)(2、1)(2、2)(2、3)(2、4)(3、1)(3、2)(3、3)(3、4)(4、1)(4、2)(4、3)(4、4),
共16个. 8分
事件B包含的结果有(1、2)(2、1)(2、2)(2、3)(2、4)(3、2)(4、2),
共7个. 10分
所以所求事件的概率为P(B)=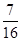 . 12分
. 12分
考点:1.随机事件的概率;2.古典概型.

 全优点练单元计划系列答案
全优点练单元计划系列答案为了对某课题进行研究,用分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
| 高校 | 相关人数 | 抽取人数 |
| A | 18 |  |
| B | 36 | 2 |
| C | 54 | 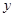 |
(1)求
 ,
,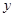 ;
;(2)若从高校B、C抽取的人中选2人作专题发言,
求这2人都来自高校C的概率.
小王经营一家面包店,每天从生产商处订购一种品牌现烤面包出售.已知每卖出一个现烤面包可获利10元,若当天卖不完,则未卖出的现烤面包因过期每个亏损5元.经统计,得到在某月(30天)中,小王每天售出的现烤面包个数 及天数如下表:
及天数如下表:
售出个数 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天数 | 3 | 3 | 3 | 6 | 9 | 6 |
(Ⅰ)计算小王某天售出该现烤面包超过13个的概率;
(Ⅱ)若在今后的连续5天中,售出该现烤面包超过13个的天数大于3天,则小王决定增加订购量. 试求小王增加订购量的概率.
(Ⅲ)若小王每天订购14个该现烤面包,求其一天出售该现烤面包所获利润的分布列和数学期望.
某市举行一次数学新课程骨干培训活动,共邀请15名使用不同版本教材的数学教师,具体情况数据如下表所示:
| 版本 | 人教A版 | 人教B版 | ||
| 性别 | 男教师 | 女教师 | 男教师 | 女教师 |
| 人数 | 6 |  | 4 | 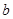 |
现从这15名教师中随机选出2名,则2人恰好是教不同版本的女教师的概率是
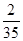 .且
.且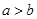 .
.(1)求实数
 ,
,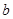 的值
的值(2)培训活动现随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为
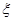 ,求随机变量
,求随机变量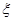 的分布列和数学期望
的分布列和数学期望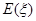 .
.  ,甲、丙两人都回答错误的概率是
,甲、丙两人都回答错误的概率是 ,乙、丙两人都回答正确的概率是
,乙、丙两人都回答正确的概率是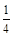 .
. 表示回答该题正确的人数,求
表示回答该题正确的人数,求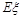 .
.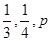 ,
, .
. 的值,
的值,