题目内容
为了调查某大学学生在周日上网的时间,随机对1OO名男生和100名女生进行了不记 名的问卷调查.得到了如下的统计结果:
表1:男生上网时间与频数分布表
表2:女生上网时间与频数分布表
(I)若该大学共有女生750人,试估计其中上网时间不少于60分钟的人数;
(II)完成下面的2x2列联表,并回答能否有90%的把握认为“学生周日上网时间与性 别有关”?
表3: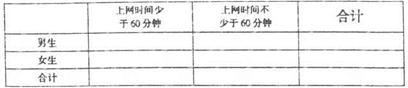

(I)225;(II)没有90%的把握认为“学生周日上网时间与性别有关”.
解析试题分析:(I)设估计上网时间不少于60分钟的人数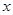 , 依据题意有
, 依据题意有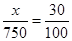 ,解得之;(II)根据男生、女生的上网时间频数分布表易得2×2列联表,并由
,解得之;(II)根据男生、女生的上网时间频数分布表易得2×2列联表,并由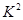 公式得出
公式得出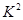 值,即得结论.
值,即得结论.
试题解析:(Ⅰ)设估计上网时间不少于60分钟的人数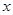 , 依据题意有
, 依据题意有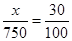 , 4分
, 4分
解得: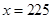 ,所以估计其中上网时间不少于60分钟的人数是225人. 6分
,所以估计其中上网时间不少于60分钟的人数是225人. 6分
(Ⅱ)根据题目所给数据得到如下列联表:
8分 上网时间少于60分钟 上网时间不少于60分钟 合计 男生 60 40 100 女生 70 30 100 合计 130 70 200
其中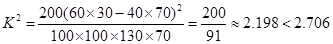 10分
10分
因此,没有90%的把握认为“学生周日上网时间与性别有关”. 12分
考点:1、频率;2、独立性检验.

 阅读快车系列答案
阅读快车系列答案甲,乙,丙三位学生独立地解同一道题,甲做对的概率为 ,乙,丙做对的概率分别为
,乙,丙做对的概率分别为 ,
, (
( >
> ),且三位学生是否做对相互独立.记
),且三位学生是否做对相互独立.记 为这三位学生中做对该题的人数,其分布列为:
为这三位学生中做对该题的人数,其分布列为:
 | 0 | 1 | 2 | 3 |
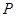 |  | 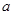 |  |  |
(Ⅱ)求
 ,
, 的值;
的值;(Ⅲ)求
 的数学期望.
的数学期望. (12分)某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生.
(Ⅰ)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(Ⅱ)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.
甲的频数统计表(部分)
| 运行 次数n | 输出y的值 为1的频数 | 输出y的值 为2的频数 | 输出y的值 为3的频数 |
| 30 | 14 | 6 | 10 |
| … | … | … | … |
| 2100 | 1027 | 376 | 697 |
| 运行 次数n | 输出y的值 为1的频数 | 输出y的值 为2的频数 | 输出y的值 为3的频数 |
| 30 | 12 | 11 | 7 |
| … | … | … | … |
| 2100 | 1051 | 696 | 353 |

某单位实行休年假制度三年来, 名职工休年假的次数进行的调查统计结果如下表所示:
名职工休年假的次数进行的调查统计结果如下表所示:
| 休假次数 |  |  |  |  |
| 人数 | 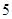 |  |  |  |
⑴从该单位任选两名职工,用
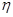 表示这两人休年假次数之和,记“函数
表示这两人休年假次数之和,记“函数 ,在区间
,在区间 ,
, 上有且只有一个零点”为事件
上有且只有一个零点”为事件 ,求事件
,求事件 发生的概率
发生的概率 ;
;⑵从该单位任选两名职工,用
 表示这两人休年假次数之差的绝对值,求随机变量
表示这两人休年假次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望 .
. 
 个,每个选择题给出了四个选项,在给出的四个选项中,只有一项是符合题目要求的. 评分标准规定:对于每个选择题,不选或多选或错选得
个,每个选择题给出了四个选项,在给出的四个选项中,只有一项是符合题目要求的. 评分标准规定:对于每个选择题,不选或多选或错选得 分,选对得
分,选对得 分.在这次考试的选择题部分,某考生比较熟悉其中的
分.在这次考试的选择题部分,某考生比较熟悉其中的 个题,该考生做对了这
个题,该考生做对了这 个题,有一个题,因全然不理解题意,该考生在给出的四个选项中,随机选了一个;有一个题给出的四个选项,可判断有一个选项不符合题目要求,该考生在剩下的三个选项中,随机选了一个;还有两个题,每个题给出的四个选项,可判断有两个选项不符合题目要求,对于这两个题,该考生都是在剩下的两个选项中,随机选了一个选项.请你根据上述信息,解决下列问题:
个题,有一个题,因全然不理解题意,该考生在给出的四个选项中,随机选了一个;有一个题给出的四个选项,可判断有一个选项不符合题目要求,该考生在剩下的三个选项中,随机选了一个;还有两个题,每个题给出的四个选项,可判断有两个选项不符合题目要求,对于这两个题,该考生都是在剩下的两个选项中,随机选了一个选项.请你根据上述信息,解决下列问题: 分的概率;
分的概率; ,求
,求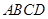 的边长为2,
的边长为2, 分别是边
分别是边 的中点.
的中点. ,求满足
,求满足 的概率;
的概率; 这八个点中,随机选取两个点,记这两个点之间的距离为
这八个点中,随机选取两个点,记这两个点之间的距离为 ,求随机变量
,求随机变量 .
.