题目内容
1.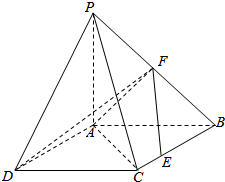 如图,四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,点F是PB的中点,点E是边BC上的任意一点.
如图,四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,点F是PB的中点,点E是边BC上的任意一点.(1)求证:AF⊥EF.
(2)若PA=2,求三棱锥P-ADF的体积.
分析 (1)由已知得PA⊥AD,PA⊥AB,AB⊥BC,从而PA⊥BC,进而BC⊥面PAB,又AF⊥PB,由此能证明AF⊥EF.
(2)利用等体积转换,求三棱锥P-ADF的体积.
解答 (1)证明:∵四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,
∴PA⊥AD,PA⊥AB,又AD∩AB=A,AB⊥BC,
∴PA⊥平面ABCD,又BC?面ABCD,∴PA⊥BC,
∵AB∩PA=A,∴BC⊥面PAB,
∴BC⊥AF,
∵△PAB是以A为直角顶点的等腰直角三角形,F是PB中点,
∴AF⊥PB,
又PB∩BC=B,∴AF⊥平面PBC,
∵EF?平面PBC,∴AF⊥EF.
(2)解:由(1)知AD∥BC,BC⊥平面PAB,
则AD⊥平面PAB,即AD⊥平面PAF
又∵PA=AB=AD=2,PA⊥AB,PA⊥AD,
∴AB=$\sqrt{P{A}^{2}+A{B}^{2}}$=2$\sqrt{2}$,
∴AF=PF=$\frac{1}{2}$PB=$\sqrt{2}$.
又AF⊥PB,∴S△PAF=$\frac{1}{2}×PF×AF$=1
∴VP-ADF=VD-PAF=$\frac{1}{3}×1×2$=$\frac{2}{3}$
即三棱锥P-ADF的体积为$\frac{2}{3}$.…(12分)
点评 本题考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
7.-268°是第( )象限的角.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
16.从边长为10cm×16cm的矩形纸板的四角截去四个相同的小正方形,做成一个无盖的盒子,则盒子容积的最大值为( )
| A. | 160 cm3 | B. | 144cm3 | C. | 72cm3 | D. | 12 cm3 |
11.抛物线x2=-4y的焦点坐标为( )
| A. | (1,0) | B. | (0,1) | C. | (-1,0) | D. | (0,-1) |