题目内容
如图所示,在 △ABC内有一内接正方形,它的一条边在斜边BC上,设AB=
△ABC内有一内接正方形,它的一条边在斜边BC上,设AB= ,∠ABC
,∠ABC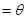

(1)求△ABC的面积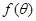 与正方形面积
与正方形面积 ;
;
(2)当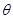 变化时,求
变化时,求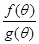 的最小值,并求出对应
的最小值,并求出对应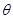 的值。
的值。
(1)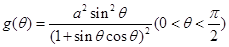
(2)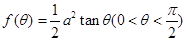 ,
, 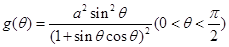 ,当
,当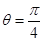 时成立,
时成立, 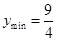 。
。
解析试题分析:(1)由题得: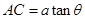
∴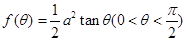 设正方形的边长为
设正方形的边长为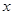 ,则
,则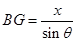 ,由几何关系知:
,由几何关系知: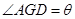 ∴
∴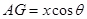 由
由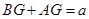
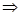
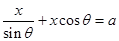
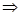
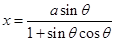
∴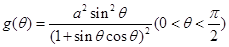
(2)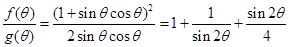 令:
令: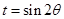 ∵
∵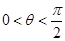
∴ ∴
∴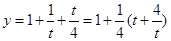 ∵函数
∵函数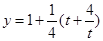 在
在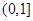 递减
递减
∴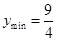 (当且仅当
(当且仅当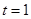 即
即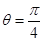 时成立)
时成立)
答: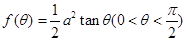
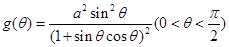
当 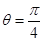 时成立
时成立 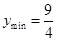
考点:本题主要考查三角函数的应用,直角三角形边角关系,三角函数和差倍半公式,“对号函数”的性质。
点评:中档题,本题利用三角形中的边角关系,逐步建立了三角形面积、正方形面积表达式,为进一步研究函数的最值奠定了基础。(2)中通过换元,转化成为求“对号函数”的最小值问题,利用函数的单调性使问题得解。

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 上的函数
上的函数 的图象关于直线
的图象关于直线 对称,当
对称,当 时,函数
时,函数 ,其图象如图
,其图象如图
 在
在 的表达式;
的表达式; 的解.
的解. .
.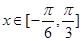 时,函数
时,函数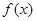 的最大值与最小值的和为
的最大值与最小值的和为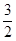 ,求
,求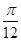 个单位,纵坐标不变横坐标变为原来的2
个单位,纵坐标不变横坐标变为原来的2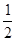 ,得到函数
,得到函数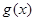 ,求
,求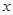 轴的正半轴、直线
轴的正半轴、直线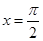 所围成图形的
所围成图形的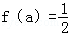 的a的值,并对此时的a值求y的最大值.
的a的值,并对此时的a值求y的最大值.

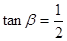 ,求
,求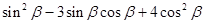 的值.
的值. 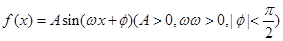 在一个周期内的图象下图所示。
在一个周期内的图象下图所示。
 ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围和这两个根的和。
有两个不同的实数根,求实数m的取值范围和这两个根的和。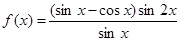 。
。 的定义域及最小正周期;
的定义域及最小正周期;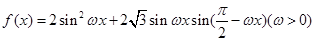 最小正周期为
最小正周期为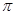
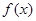 的单调递增区间及对称中心坐标
的单调递增区间及对称中心坐标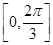 上的取值范围。
上的取值范围。