题目内容
设关于x的函数y=2cos2x﹣2acosx﹣(2a+1)的最小值为f(a),试确定满足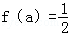 的a的值,并对此时的a值求y的最大值.
的a的值,并对此时的a值求y的最大值.
a=﹣1, 此时ymax=﹣4a+1=5.
解析试题分析:令cosx=t,t∈[﹣1,1], 则y=2t2﹣2at﹣(2a+1),对称轴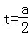 ,
,
当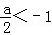 ,即a<﹣2时,[﹣1,1]是函数y的递增区间,
,即a<﹣2时,[﹣1,1]是函数y的递增区间,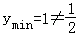 ;
;
当 ,即a>2时,[﹣1,1]是函数y的递减区间,
,即a>2时,[﹣1,1]是函数y的递减区间,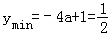 ,
,
得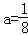 ,与a>2矛盾;
,与a>2矛盾;
当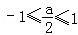 ,即﹣2≤a≤2时,
,即﹣2≤a≤2时,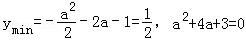
得a=﹣1,或a=﹣3,
∴a=﹣1, 此时ymax=﹣4a+1=5.
考点:三角函数的性质
点评:解决的关键是利用三角函数的单调性来求解最值,属于基础题。

练习册系列答案
相关题目
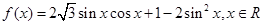 .
. 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;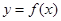 的图像上各点的纵坐标保持不变,横坐标缩短到原来的
的图像上各点的纵坐标保持不变,横坐标缩短到原来的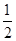 ,把所得到的图像再向左平移
,把所得到的图像再向左平移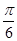 单位,得到的函数
单位,得到的函数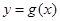 的图像,求函数
的图像,求函数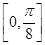 上的最小值.
上的最小值.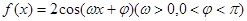 的图像上的每一点的横坐标伸长为原来的2倍,纵坐标不变,然后再向左平移
的图像上的每一点的横坐标伸长为原来的2倍,纵坐标不变,然后再向左平移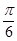 个单位后得到一个最小正周期为
个单位后得到一个最小正周期为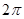 的奇函数
的奇函数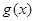 。
。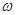 和
和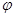 的值
的值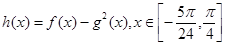 的最大值与最小值。
的最大值与最小值。 的图像上两相邻最高点的坐标分别为
的图像上两相邻最高点的坐标分别为 .
.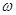 的值;
的值; 分别是角A,B,C的对边,且
分别是角A,B,C的对边,且 求
求 的取值范围.
的取值范围.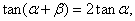 求证:
求证: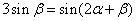 .
.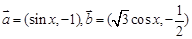 ,函数
,函数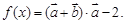
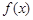 的最小正周期T及单调减区间;
的最小正周期T及单调减区间;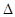 ABC内角A,B,C的对边,其中A为锐角,
ABC内角A,B,C的对边,其中A为锐角,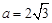 ,
,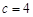 ,且
,且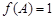 .求A,b的长和
.求A,b的长和 △ABC内有一内接正方形,它的一条边在斜边BC上,设AB=
△ABC内有一内接正方形,它的一条边在斜边BC上,设AB= ,∠ABC
,∠ABC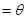

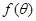 与正方形面积
与正方形面积 ;
;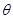 变化时,求
变化时,求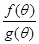 的最小值,并求出对应
的最小值,并求出对应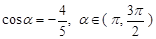 ,求
,求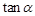 .
. 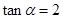 ,求
,求 的值.
的值. 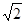 sin(2x+
sin(2x+ ),x∈R.
),x∈R.