题目内容
如图,摩天轮的半径为50 m,点O距地面的高度为60 m,摩天轮做匀速转动,每3 min转一圈,摩天轮上点P的起始位置在最低点处.
(1)试确定在时刻t(min)时点P距离地面的高度;
(2)在摩天轮转动的一圈内,有多长时间点P距离地面超过85 m?
(1) y=60-50cos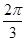 t (t≥0) (2) 在摩天轮转动的一圈内,点P距离地面超过85 m的时间有1分钟.
t (t≥0) (2) 在摩天轮转动的一圈内,点P距离地面超过85 m的时间有1分钟.
解析试题分析:(1)解:设点P离地面的距离为y,则可令 y=Asin(ωt+φ)+b.
由题设可知A=50,b=60. 2分
又T=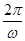 =3,所以ω=
=3,所以ω=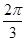 ,从而y=50sin(
,从而y=50sin(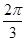 t+φ)+60. 4分
t+φ)+60. 4分
再由题设知t=0时y=10,代入y=50sin(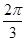 t+φ)+60,得sinφ=-1,从而φ=-
t+φ)+60,得sinφ=-1,从而φ=-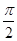 .
.
6分
因此,y=60-50cos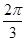 t (t≥0). 8分
t (t≥0). 8分
(2)要使点P距离地面超过85 m,则有y=60-50cos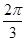 t>85,即cos
t>85,即cos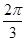 t<-
t<- .
.
10分
于是由三角函数基本性质推得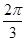 <
<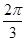 t<
t<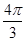 ,即1<t<2. 12分
,即1<t<2. 12分
所以,在摩天轮转动的一圈内,点P距离地面超过85 m的时间有1分钟.
14分
考点:三角函数的运用
点评:解决的关键是利用摩天轮的转动有周期性,以及点的坐标的表示来得到解析式,属于基础题。

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目

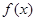 的最小正周期及单调递增区间;
的最小正周期及单调递增区间; 中,若
中,若 ,
, ,
, ,求
,求 的值.
的值.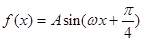 (其中
(其中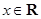 ,
,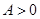 ,
,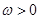 )的最大值为2,最小正周期为
)的最大值为2,最小正周期为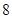 .
.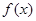 的解析式;
的解析式;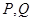 的横坐标依次为
的横坐标依次为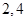 ,
,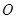 为坐标原点,求
为坐标原点,求 的值.
的值.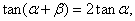 求证:
求证: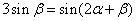 .
. 在
在 处取最小值.
处取最小值. 的值;
的值; ABC中,
ABC中, 分别是角A,B,C的对边,已知
分别是角A,B,C的对边,已知
 ,求值
,求值 .
. △ABC内有一内接正方形,它的一条边在斜边BC上,设AB=
△ABC内有一内接正方形,它的一条边在斜边BC上,设AB= ,∠ABC
,∠ABC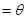

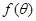 与正方形面积
与正方形面积 ;
;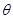 变化时,求
变化时,求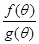 的最小值,并求出对应
的最小值,并求出对应 ,求该函数的最大值和最小值以及取得最值时的
,求该函数的最大值和最小值以及取得最值时的 的值.
的值. 的扇形,作为圆锥的侧面,求圆锥的表面积和体积.
的扇形,作为圆锥的侧面,求圆锥的表面积和体积.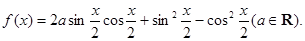
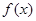 的最小正周期及图象的对称轴方程式;
的最小正周期及图象的对称轴方程式;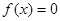 的条件下,求
的条件下,求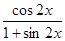 的值.
的值.