题目内容
6.在等差数列{an}中,a1+a3+a5=-3,a1•a3•a5=15,求它的通项公式.分析 由等差数列的性质,求出首项和公差,继而得到通项公式
解答 解:等差数列{an}中,设公差为d,2a3=a1+a5
∵a1+a3+a5=-3,a1•a3•a5=15,
∴a3=-1,且(-1-2d)•(-1)•(-1+2d)=15,
解得d2=4,∴d=2,或d=-2,
当d=2时,a1=a3-2d=-1-4=-5,
∴an=-5+(n-1)×2=2n-7,
当d=-2时,a1=a3-2d=-1+4=3,
∴an=3+(n-1)×(-2)=-2n+5.
点评 本题考查数列的通项公式的求法,是基础题,解题时要认真审题,注意等差数列的通项公式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
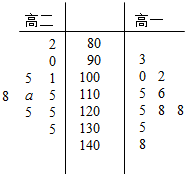 高三学生小周把自己在高二时的10次数学考试成绩和高三时的10次数学考试成绩(试卷总分150分)进行统计,统计数据用茎叶图表示(如图所示)
高三学生小周把自己在高二时的10次数学考试成绩和高三时的10次数学考试成绩(试卷总分150分)进行统计,统计数据用茎叶图表示(如图所示)