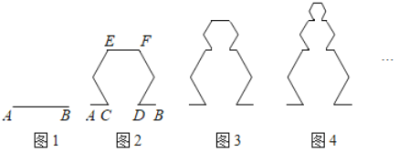
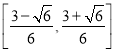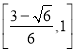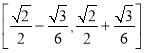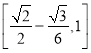题目内容
【题目】以直角坐标系的原点为极点，
轴的非负半轴为极轴建立极坐标系，曲线
的极坐标方程为
，直线
的参数方程为
（
为参数）.
（1）求曲线的参数方程与直线的普通方程；
（2）设点过
为曲线上的动点，点
和点
为直线上的点，且满足
为等边三角形，求边长的取值范围.
【答案】（1）
：
（
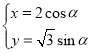为参数，
），
：
；（2）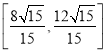
【解析】
（1）利用公式即可容易化简曲线的方程为直角坐标方程，再写出其参数方程即可；利用消参即可容易求得直线的普通方程；
（2）设出
的坐标的参数形式，将问题转化为求点到直线距离的范围问题，利用三角函数的值域求解即可容易求得结果.
（1）曲线的极坐标方程为
，
故可得
，则
，
整理得
，也即
，
由
，则可得
，
故其参数方程为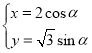
（为参数，）；
又直线的参数方程为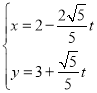
，
故可得其普通方程为.
（2）不妨设点的坐标为
，
则点到直线的距离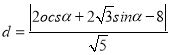
，
，
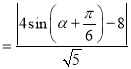容易知
在区间
的值域为
，
故可得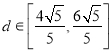
.
则三角形
的边长为
，故其范围为.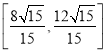
【题目】笔、墨、纸、砚是中国独有的文书工具，即“文房四宝”．笔、墨、纸、砚之名，起源于南北朝时期，其中的“纸”指的是宣纸，宣纸“始于唐代，产于泾县”，而唐代泾县隶属于宣州府管辖，故因地而得名“宣纸”，宣纸按质量等级，可分为正牌和副牌（优等品和合格品），某公司年产宣纸10000刀，公司按照某种质量标准值x给宣纸确定质量等级，如表所示：
x | （48，52] | （44，48]∪（52，56] | （0，44]∪（56，100] |
质量等级 | 正牌 | 副牌 | 废品 |
公司在所生产的宣纸中随机抽取了一刀（100张）进行检验，得到频率分布直方图如图所示，已知每张正牌纸的利润是10元，副牌纸的利润是5元，废品亏损10元．
（Ⅰ）按正牌、副牌、废品进行分层抽样，从这一刀（100张）纸中抽出一个容量为5的样本，再从这个样本中随机抽出两张，求其中无废品的概率；
（Ⅱ）试估计该公司生产宣纸的年利润（单位：万元）．
