题目内容
 [选做题]本题包括A、B、C、D共4小题,请从这4小题中选做2小题,每小题10分,共20分.
[选做题]本题包括A、B、C、D共4小题,请从这4小题中选做2小题,每小题10分,共20分.A.如图,AD是∠BAD的角平分线,⊙O过点A且与BC边相切于点D,与AB,AC分别交于E、F两点.求证:EF∥BC.
B.已知M=
|
C.已知直线l的极坐标方程为θ=
| π |
| 4 |
|
D.设函数f(x)=|x-2|+|x+2|,若不等式|a+b|-|4a-b|≤|a|,f(x)对任意a,b∈R,且a≠0恒成立,求实数x的取值范围.
分析:A.证明EF∥BC,只要证明内错角相等,即∠DEF=∠EDB即可;
B.设出M的逆矩阵,利用MM-1=E,建立等式,由此可求矩阵的逆矩阵;
C.直线l的极坐标方程化为直角坐标方程,曲线C
(α为参数)化为普通方程,求出圆心到直线y=x的距离,即可求出弦长;
D.利用绝对值不等式的性质,再将|a+b|-|4a-b|≤|a|f(x)对任意a,b∈R,且a≠0恒成立,转化为f(x)≥5,即可确定
x的取值范围.
B.设出M的逆矩阵,利用MM-1=E,建立等式,由此可求矩阵的逆矩阵;
C.直线l的极坐标方程化为直角坐标方程,曲线C
|
D.利用绝对值不等式的性质,再将|a+b|-|4a-b|≤|a|f(x)对任意a,b∈R,且a≠0恒成立,转化为f(x)≥5,即可确定
x的取值范围.
解答:A.证明:连接DE,可得∠DEF=∠DAC
∵AD是∠BAC的平分线
∴∠EAD=∠EDB
∴∠DEF=∠EDB
∴EF∥BC
B.设M-1=
,依题意,有
=
∴
=
∴
∴
∴M-1=
C.直线l的极坐标方程为θ=
(ρ∈R)的直角坐标方程为y=x,曲线C
(α为参数)的普通方程为(x-1)2+(y-2)2=4,所以圆心(1,2)到直线y=x的距离d=
=
∴AB=2
=
D.∵a≠0,∴a>0
∴|a+b|-|4a-b|≤|(a+b)+(4a-b)|=5|a|=5a,
∵|a+b|-|4a-b|≤|a|f(x)对任意a,b∈R,且a≠0恒成立,
∴5a≤af(x)
∴f(x)≥5
∴x≤-2.5或x≥2.5
∴x的取值范围是x≤-2.5或x≥2.5.
∵AD是∠BAC的平分线
∴∠EAD=∠EDB
∴∠DEF=∠EDB
∴EF∥BC
B.设M-1=
|
|
|
|
∴
|
|
∴
|
∴
|
∴M-1=
|
C.直线l的极坐标方程为θ=
| π |
| 4 |
|
| |1-2| | ||
|
| ||
| 2 |
∴AB=2
4-
|
| 14 |
D.∵a≠0,∴a>0
∴|a+b|-|4a-b|≤|(a+b)+(4a-b)|=5|a|=5a,
∵|a+b|-|4a-b|≤|a|f(x)对任意a,b∈R,且a≠0恒成立,
∴5a≤af(x)
∴f(x)≥5
∴x≤-2.5或x≥2.5
∴x的取值范围是x≤-2.5或x≥2.5.
点评:本题是选作题,考查几何证明选讲,考查逆矩阵,考查坐标系与参数方程,考查绝对值不等式,综合性强.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
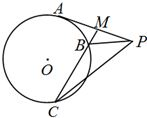 选做题本题包括A,B,C,D四小题,请选定其中 两题 作答,每小题10分,共计20分,
选做题本题包括A,B,C,D四小题,请选定其中 两题 作答,每小题10分,共计20分, (2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
(2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. 选修4-1:几何证明选讲
选修4-1:几何证明选讲 ,N=
,N= ,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。
,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。 。
。 ,矩阵A属于特征值λ1=-1的一个特征向量为
,矩阵A属于特征值λ1=-1的一个特征向量为 ,属于特征值λ2=4的一个特征向量为
,属于特征值λ2=4的一个特征向量为 .求矩阵A.
.求矩阵A. .以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
.以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 .点
.点 的最小值.
的最小值.