题目内容
 (2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
(2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.A.选修4-1:几何证明选讲
如图,已知AB,CD是圆O的两条弦,且AB是线段CD的 垂直平分线,若AB=6,CD=2
| 5 |
B.选修4-2:矩阵与变换(本小题满分10分)
已知矩阵M=
|
C.选修4-4:坐标系与参数方程(本小题满分10分)
在平面直角坐标系xOy中,已知曲线C的参数方程是
|
D.选修4-5:不等式选讲(本小题满分10分)
已知关于x的不等式|ax-1|+|ax-a|≥1的解集为R,求正实数a的取值范围.
分析:A:设AB和 CD交与点E,设AE=x,由题意可得AB是直径,EB=6-x,CE=5.由射影定理求出x的值,从而求得AC的值.
B:由矩阵M=
的一个特征值是3,求得 a=2,M=
.设直线x-2y-3=0上的任意一点(x,y)在M作用下的对应点为(x′,y′),则有
=
,
即
,代人x-2y-3=0,整理可得新直线方程.
C:由参数方程消去参数,化为普通方程,求出圆心和半径,可得在极坐标系下,曲线C是以(1,
)为圆心,半径等于1的圆,从而求得它的极坐标方程.
D:因为|ax-1|+|ax-a|≥|a-1|,故原不等式解集为R,等价于|a-1|≥1,由此求得a的范围,即为所求.
B:由矩阵M=
|
|
|
|
|
即
|
C:由参数方程消去参数,化为普通方程,求出圆心和半径,可得在极坐标系下,曲线C是以(1,
| π |
| 2 |
D:因为|ax-1|+|ax-a|≥|a-1|,故原不等式解集为R,等价于|a-1|≥1,由此求得a的范围,即为所求.
解答:解:A:连接BC,设AB和 CD交与点E,设AE=x,∵AB是线段CD的 垂直平分线,故AB是直径,∠ACB=90°,故 EB=6-x,CE=5.
由射影定理可得 CE2=AE•EB,即 x(6-x)=5,解得x=1(舍去),或 x=5.
∴AC2=AE•AB=5×6=30,∴AC=
.
B:∵已知矩阵M=
的一个特征值是3,∴f(λ)=
=(λ-2)(λ-a)-1=0,即 (3-2)(3-a)-1=0,
解得a=2,∴M=
.
设直线x-2y-3=0上的任意一点(x,y)在M作用下的对应点为(x′y′,),
则有
=
,整理得
,即
,代人x-2y-3=0,整理得4x'-5y'-9=0,
故所求直线方程为:4x-5y-9=0.
C:由
消去θ,得x2+(y-1)2=1,
曲线C是以(0,1)为圆心,半径等于1的圆.
所以在极坐标系下,曲线C是以(1,
)为圆心,半径等于1的圆.
所以曲线C的极坐标方程是ρ=2sinθ.
D:因为|ax-1|+|ax-a|≥|a-1|,故原不等式解集为R等价于|a-1|≥1.所以a≥2,或a≤0.
又因为a>0,所以a≥2,所以正实数a的取值范围为[2,+∞).
由射影定理可得 CE2=AE•EB,即 x(6-x)=5,解得x=1(舍去),或 x=5.
∴AC2=AE•AB=5×6=30,∴AC=
| 30 |
B:∵已知矩阵M=
|
|
解得a=2,∴M=
|
设直线x-2y-3=0上的任意一点(x,y)在M作用下的对应点为(x′y′,),
则有
|
|
|
|
|
故所求直线方程为:4x-5y-9=0.
C:由
|
曲线C是以(0,1)为圆心,半径等于1的圆.
所以在极坐标系下,曲线C是以(1,
| π |
| 2 |
所以曲线C的极坐标方程是ρ=2sinθ.
D:因为|ax-1|+|ax-a|≥|a-1|,故原不等式解集为R等价于|a-1|≥1.所以a≥2,或a≤0.
又因为a>0,所以a≥2,所以正实数a的取值范围为[2,+∞).
点评:本题主要考查绝对值不等式的解法,与圆有关的比例线段,矩阵的特征值与特征向量,圆的参数方程、极坐标方程的应用,属于中档题.

练习册系列答案
相关题目
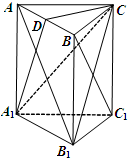 (2013•宿迁一模)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,BC=BB1,D为AB的中点.
(2013•宿迁一模)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,BC=BB1,D为AB的中点.