题目内容
选做题本题包括A,B,C,D四小题,请选定其中 两题 作答,每小题10分,共计20分,解答时应写出文字说明,证明过程或演算步骤.
A选修4-1:几何证明选讲
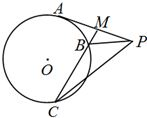
自圆O外一点P引圆的一条切线PA,切点为A,M为PA的中点,过点M引圆O的割线交该圆于B、C两点,且∠BMP=100°,∠BPC=40°,求∠MPB的大小.
B选修4-2:矩阵与变换
已知二阶矩阵A=
 ,矩阵A属于特征值λ1=-1的一个特征向量为
,矩阵A属于特征值λ1=-1的一个特征向量为 ,属于特征值λ2=4的一个特征向量为
,属于特征值λ2=4的一个特征向量为 .求矩阵A.
.求矩阵A.C选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,已知曲线C的参数方程为
 .以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
.以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 .点
.点P为曲线C上的动点,求点P到直线l距离的最大值.
D选修4-5:不等式选讲
若正数a,b,c满足a+b+c=1,求
 的最小值.
的最小值.
【答案】分析:A:根据MA为圆O的切线,由切割线定理得MA2=MB•MC.从而MP2=MB•MC.依据相似三角形的判定方法得:△BMP∽△PMC得出∠MPB=∠MCP.最后在△MCP中,即得∠MPB.
B:由特征值、特征向量定义可知,Aα1=λ1α1,得关于a,b的方程,解得a,b,c,d即可得矩阵.
C:先将原极坐标方程化简为ρcosθ+ρsinθ=4,再化成直线l的直角坐标方程,设点P的坐标为(2cosα,sinα),利用点到直线l的距离结合三角函数的有界性即可;
D:利用柯西不等式结合正数a,b,c满足a+b+c=1,得出 ,从而得出原式取最小值.
,从而得出原式取最小值.
解答:解:A
因为MA为圆O的切线,所以MA2=MB•MC.
又M为PA的中点,所以MP2=MB•MC.
因为∠BMP=∠PMC,所以△BMP∽△PMC.(5分)
于是∠MPB=∠MCP.
在△MCP中,由∠MPB+∠MCP+∠BPC+∠BMP=180°,得∠MPB=20°.(10分)
B:
由特征值、特征向量定义可知,Aα1=λ1α1,
即 ,得
,得 (5分)
(5分)
同理可得 解得a=2,b=3,c=2,d=1.因此矩阵A=
解得a=2,b=3,c=2,d=1.因此矩阵A= .(10分)
.(10分)
C:
 化简为ρcosθ+ρsinθ=4,
化简为ρcosθ+ρsinθ=4,
则直线l的直角坐标方程为x+y=4.(4分)
设点P的坐标为(2cosα,sinα),得P到直线l的距离 ,
,
即 ,其中
,其中 .(8分)
.(8分)
当sin(α+φ)=-1时, .(10分)
.(10分)
D:
因为正数a,b,c满足a+b+c=1,
所以, ,(5分)
,(5分)
即 ,
,
当且仅当3a+2=3b+2=3c+2,即 时,原式取最小值1.(10分)
时,原式取最小值1.(10分)
点评:本小题主要考查特征值与特征向量的计算、相似三角形的判定、简单曲线的极坐标方程、不等式的证明等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.
B:由特征值、特征向量定义可知,Aα1=λ1α1,得关于a,b的方程,解得a,b,c,d即可得矩阵.
C:先将原极坐标方程化简为ρcosθ+ρsinθ=4,再化成直线l的直角坐标方程,设点P的坐标为(2cosα,sinα),利用点到直线l的距离结合三角函数的有界性即可;
D:利用柯西不等式结合正数a,b,c满足a+b+c=1,得出
 ,从而得出原式取最小值.
,从而得出原式取最小值.解答:解:A
因为MA为圆O的切线,所以MA2=MB•MC.
又M为PA的中点,所以MP2=MB•MC.
因为∠BMP=∠PMC,所以△BMP∽△PMC.(5分)
于是∠MPB=∠MCP.
在△MCP中,由∠MPB+∠MCP+∠BPC+∠BMP=180°,得∠MPB=20°.(10分)
B:
由特征值、特征向量定义可知,Aα1=λ1α1,
即
 ,得
,得 (5分)
(5分)同理可得
 解得a=2,b=3,c=2,d=1.因此矩阵A=
解得a=2,b=3,c=2,d=1.因此矩阵A= .(10分)
.(10分)C:
 化简为ρcosθ+ρsinθ=4,
化简为ρcosθ+ρsinθ=4,则直线l的直角坐标方程为x+y=4.(4分)
设点P的坐标为(2cosα,sinα),得P到直线l的距离
 ,
,即
 ,其中
,其中 .(8分)
.(8分)当sin(α+φ)=-1时,
 .(10分)
.(10分)D:
因为正数a,b,c满足a+b+c=1,
所以,
 ,(5分)
,(5分)即
 ,
,当且仅当3a+2=3b+2=3c+2,即
 时,原式取最小值1.(10分)
时,原式取最小值1.(10分)点评:本小题主要考查特征值与特征向量的计算、相似三角形的判定、简单曲线的极坐标方程、不等式的证明等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
相关题目
 选做题本题包括A,B,C,D四小题,请选定其中 两题 作答,每小题10分,共计20分,
选做题本题包括A,B,C,D四小题,请选定其中 两题 作答,每小题10分,共计20分, (2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
(2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. [选做题]本题包括A、B、C、D共4小题,请从这4小题中选做2小题,每小题10分,共20分.
[选做题]本题包括A、B、C、D共4小题,请从这4小题中选做2小题,每小题10分,共20分. 选修4-1:几何证明选讲
选修4-1:几何证明选讲 ,N=
,N= ,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。
,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。 。
。