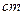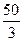题目内容
(本题满分10分)选修4-1:几何证明选讲
如图,圆O的直径AB=10,弦DE⊥AB于点H,
AH=2.
(Ⅰ)求DE的长;
(Ⅱ)延长ED到P,过P作圆O的切线,切点为C,
若PC=2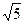 ,求PD的长.
,求PD的长.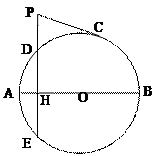
如图,圆O的直径AB=10,弦DE⊥AB于点H,
AH=2.
(Ⅰ)求DE的长;
(Ⅱ)延长ED到P,过P作圆O的切线,切点为C,
若PC=2
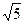 ,求PD的长.
,求PD的长.
解:(Ⅰ)连接AD,DB,由于AB为圆O的直径,∴ÐAD^DB.………2分
又AB⊥DE,DH=HE,
∴DH2=AH×BH=2(10-2)=16, …………4分
DH=4,DE=8. …………5分
(Ⅱ)PC切圆O于点C,PC2=PD×PE, …………7分
由切割线定理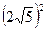 =PD·(PD+8), …………9分
=PD·(PD+8), …………9分
解得PD=2. …………10分
又AB⊥DE,DH=HE,
∴DH2=AH×BH=2(10-2)=16, …………4分
DH=4,DE=8. …………5分
(Ⅱ)PC切圆O于点C,PC2=PD×PE, …………7分
由切割线定理
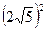 =PD·(PD+8), …………9分
=PD·(PD+8), …………9分解得PD=2. …………10分
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
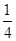 PD.则CD=________。
PD.则CD=________。 •BD
•BD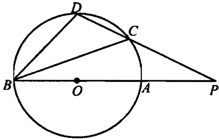
 于F,则
于F,则 EF︰BE=( )
EF︰BE=( )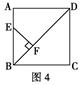
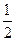
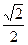
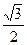
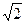
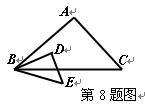
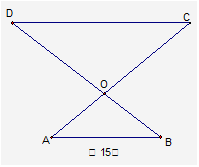
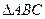 是等腰直角三角形,
是等腰直角三角形,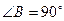 ,
,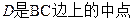 ,
,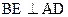 ,延长
,延长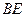 交
交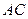 于
于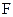 ,连接
,连接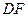 ,求证:
,求证: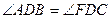

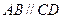 则
则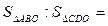 ____________.
____________.
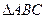 和
和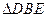 中,
中,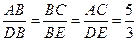 ,若
,若 ,则
,则