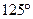题目内容
(选修4-1:几何证明选讲)
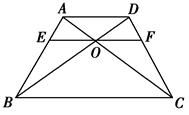
如图,BA是⊙O的直径,AD是切线,BF、BD是割线,
求证:BE•BF=BC •BD
•BD
如图,BA是⊙O的直径,AD是切线,BF、BD是割线,
求证:BE•BF=BC
 •BD
•BD连接CE,过B作⊙O的切线BG,则BG∥AD ∴∠GBC=∠FDB,又∠GBC=∠CEB
∴∠CEB=∠FDB 又∠CBE是△BCE和△BDF的公共角 ∴△BC E∽△BDF
E∽△BDF
∴ ,即BE•BF=BC•BD。
,即BE•BF=BC•BD。
∴∠CEB=∠FDB 又∠CBE是△BCE和△BDF的公共角 ∴△BC
 E∽△BDF
E∽△BDF ∴
 ,即BE•BF=BC•BD。
,即BE•BF=BC•BD。略

练习册系列答案
相关题目






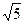 ,求PD的长.
,求PD的长.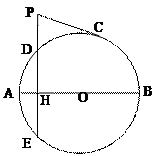
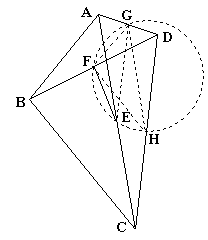
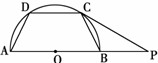
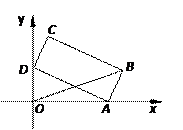 如图,矩形
如图,矩形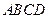 的长
的长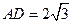 ,宽
,宽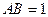 ,
,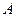 ,
,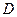 两点分别在
两点分别在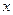 ,
,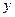 轴的正半轴上移动,
轴的正半轴上移动,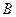 ,
,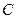 两点在第一象限.求
两点在第一象限.求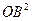 的最大值.
的最大值.
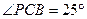 ,则
,则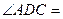 ( )
( )
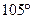
 B.
B.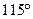 C.
C.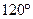 D.
D.