题目内容
3.已知△ABC是直角三角形,斜边BC的中点为M,试建立适当的直角坐标系,证明:|AM|=$\frac{1}{2}$|BC|.分析 通过建立平面直角坐标系,设出B、C坐标,利用中点坐标公式以及距离公式求解即可.
解答 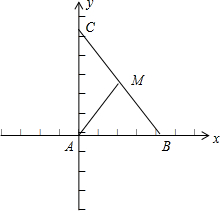 解:如图:设B(a,0),C(0,b),由中点坐标公式可得M($\frac{a}{2},\frac{b}{2}$),
解:如图:设B(a,0),C(0,b),由中点坐标公式可得M($\frac{a}{2},\frac{b}{2}$),
则|AM|=$\sqrt{(\frac{a}{2})^{2}+(\frac{b}{2})^{2}}$=$\frac{1}{2}\sqrt{{a}^{2}+{b}^{2}}$.
$\frac{1}{2}$|BC|=$\frac{1}{2}$$\sqrt{{(a-0)}^{2}+{(0-b)}^{2}}$=$\frac{1}{2}\sqrt{{a}^{2}+{b}^{2}}$.
∴|AM|=$\frac{1}{2}$|BC|.
点评 本题考查解析法证明平面集合问题,两点间距离公式的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.如果执行如图的程序框图,输出的结果为( )


| A. | 43 | B. | 69 | C. | 72 | D. | 54 |
13.在等差数列{an}中,a3+a5+a7=90,则2a6-a7等于( )
| A. | 30 | B. | 24 | C. | 20 | D. | 15 |